
iSMART〜Automatic Differentiation in Julia Final
九谷広場でJulia版ADモジュールの開発に悪戦苦闘していた日曜の午後、騒がしい排気音に集中力が途切れがちになる。当初は気に止めずにいたが女性陣が騒ぎ出したのを機に外に目を向けるとロゴを付けた旧車が何台も駆け抜けている。何事だと外に出て交通整理の係員に問いかけると、初めて北陸で開催される車イベントで堺正章さんも参画。今晩ここに泊まって明朝ゴールの京都へ向かうと聞く。目を凝らしてロゴをみると”La Festa Primavera 2023″とある。あの本邦一格式の高いイベントかと驚く。明朝出発セレモニーで往年の名車に出会えると思うと、ハイな気分になり一気にモジュールの開発が捗り完成する。さて、Julia版ADモジュールのご紹介を兼ねたJulia言語概要解説編をお届けします。On a Sunday afternoon, while I am struggling to develop Julia’s version of the AD module at Kutani Square, the loud exhaust noises cause me to lose my concentration. I don’t pay attention at first, but then I look outside and see a bunch of old cars with logo stickers driving by as the women start to make a fuss. I go outside to ask an event staffer at the traffic control what’s going on. It turns out that this is the first car event in Hokuriku that Sakai Masaaki san is participating in, and that they are staying here tonight and leaving for Kyoto tomorrow morning. I look closely at a logo sticker and read “La Festa Primavera 2023”. I am surprised to learn that this is the most prestigious automobile event in Japan. Thinking about a departure ceremony tomorrow morning, I get into a good mood, and I finally complete the development of the AD module. This is an introduction to the Julia version of the in-house AD module and also serves as an abstract of the Julia language.
La Festa Primavera 2023
日課の早朝散歩を出かける途中、瑠璃光の駐車場で出発準備中の旧車を目にする。散歩は止めて出発セレモニーを鑑賞することに。約70台の往年の名車が田圃に囲まれた中で蒼然と並ぶ景観は壮観というか異様な雰囲気である。意外と新しいナンバーが多いことに気づく。
300SL、Aston Martin DB6、356 Speedsterのエンジン音を聞くのは初めて。否応なく気持ちが昂ぶる。
356はPorsche特有の個性の有る音は耳に馴染みがある。
300SLとDB6は今風の静かな音色。その他旧車は騒がしい音一色。本邦から参加しているToyota 2000GT、Sports800も静かな音色で之といった特徴はない。



7時にゼッケン番号順に出発する。
軽快な走り出し。
唯一、黒い排煙を出しながら走り出す300SLの姿は、石原裕次郎が運転する「300SLが渋谷の交差点を黒い排煙を出しながら抜けて行った」、雑誌の記事を思い出す。



憧れの300SLは車体が色褪せている印象をもった為か、日本自動車博物館で観た当時のような感動は覚えず。本邦勢は概して一様に不格好でデザインの完成度は低い(失礼)。
期待していなかったイベントに出会い、一生忘れられない春の珍事となった事は間違いない。
15分ほどでセレモニーは終える。
AD Module in Julia
Python版自動微分に続き、新たにJulia版を実装したのでその仔細を紹介する。
端的に、Julia言語を用いたモジュールを組込むのは相当言語に関わる知識を持っていないと難しい。Just-In-Timeコンパイラーの宿痾かもしれないが、型宣言の整合性・系統性が厳しく問われる。その点Pythonは容易であった。
Juliaは比較的新しい言語故、参考資料が少なく、又ネット情報は不確かな恐れがある、本家の公式ドキュメント(1500ページ超)をざっと斜め読みすべきであろう。又、コーディング最中、Julia REPLにて”?”押下してsyntaxを幾度チェックしたことか。
help?> struct
search: struct isstructtype 'mutable struct' unsafe_trunc
struct
The most commonly used kind of type in Julia is a struct, specified as a name and a set of fields.
struct Point
x
y
end
Fields can have type restrictions, which may be parameterized:
struct Point{X}
x::X
y::Float64
end
A struct can also declare an abstract super type via <: syntax:
struct Point <: AbstractPoint
x
y
end
structs are immutable by default; an instance of one of these types cannot be modified after construction. Use mutable struct instead to declare a type whose instances can be
modified.
See the manual section on Composite Types for more details, such as how to define constructors.新人の頃先達の技術を盗めと良く言われた。品良く言うと、石井ふく子プロデューサー曰く”真似ぶ”の世界だ。今はそんな環境にない故、NotableなCodeを参照するのが最も手っ取り早く方向性に間違いが生じ難い。
Julia言語を用いたADパッケージはJulia純正の”ForwardDiff”と”AutoGrad”が周知である。素人の俺にとって”AutoGrad”は”ForwardDiff”に比べて理解しやすく、ADモジュールの実装方法について多くを学んだ。実装の途中でC++風多重定義(Multiple Dispatch)を主体に組み込むテクニックに出会う。その簡潔な手法に驚き回り回って二種のコードを作成するに至る。多重定義に基づく自家製コードは150行程度の簡素なものであるものの、その実効性は素晴らしい。
AD Constructor
先ず、Python版Overloadを適用したADモジュールをJuliaにConvertする方法についてADクラスの構築に当たり、C言語風に”struct”構文を用いることになる。
”struct”は”immutable”故、構造体メンバー変数の値を変更する場合には、”mutable”をつける必要がある。その場合、演算速度は低下するのでその使用は極力使用を避けなければならない。依って、構造体の外部にて任意の関数”variableFAD”で入力値の引受と偏微分値の設定(入力値に応じてベクトル)を行っている。尚、後述する”LocalAD”モジュールでは変更の必要がないので”struct”内部で直に設定している。”struct”構築の事例で確認してみよう。
struct ADI{T<:Real} #mutable
val::{T}
der::{T}
ADI() = new() #unnecessary constructor
endここで、”new”構文でコンストラクターを盛り込んでいるが、Pyhtonのクラスの初期化構文”def __init__(self, …)”を意識したものであるが、通常は記載しない。
尚、定義する対象の構造体に対して”abstract type”な新たな定義を行う場合、事前に”abstract type”の名称を定義しておき、 構造体宣言時にその名称で宣言する。例えば、以下のように記載する。
abstract type AbstractCustom end
struct ADI <: AbstratCustom
val #::Float64, Vector{Float64}, etc
der #::Vector{SparseMatrixCSC{Float64, Int64}}, Vector{AbstratCustom}, etc
ADI() = new() #unnecessary constructor
end構造体に対して型指定を行う方がCompileの最適化が促進される為推奨される。実装に際して、”der”メンバーに対しては、下記に紹介する”variableFAD”関数にて宣言しているように、”::Vector{SparseMatrixCSC{Float64, Int64}}”にて宣言できることを確認している一方、”val”メンバーについては型処理対応に難儀したので敢えて盛り込まなかった。己の技術力の低さを痛感。
以上、AD構造体の宣言に関わる要の論点である。
実装に関する理論的な解説は資源国ノルウエーの工科大学の修士論文が役にたつので仔細は同資料(5)をReferして頂くのが最良であるが、てっとり早く掻い摘んで以下に説明する。
Implementation #1: Forward AD
自動微分を3変数(variableFAD)と仮定すると、第一偏導関数の配列は3x3で構成される。多変数になるに従って偏導関数の配列は巨大になり演算負荷は高くなってくる。Julia純正モジュール”ForwardDiff”に対して疎行列を対応させることで演算負荷を低減できることを検証している(“ForwardAutoDiff(FAD)”)。
お手製のヤコビアンの疎行列ルーチンを導入することで軽微であるものの演算負荷の更なる低減を達成している(“CustomJacobianAutoDiff (CJAD)”)。同論文Figure 4.1を参照のこと。
SparseArraysを導入する(using SparseArrays)ことによって疎行列を効率的に取扱うことができるが、ADモジュールにも適用しているので簡単だが触れておく。
配列はCSCフォーマット(SparseMatrixCSC{Tv,Ti})で格納される。俺は多用していないので詳細は省くが、一部Julis Documentより引用した事例を記す。
julia> sparse(1:3,1:3,1.0) #Sparse format
3×3 SparseMatrixCSC{Float64, Int64} with 3 stored entries:
1.0 ⋅ ⋅
⋅ 1.0 ⋅
⋅ ⋅ 1.0
julia> a = sparse(1.0I, 3, 3) # sparse(Matrix(1.0I, 3, 3)) || sparse([1. 0. 0.; 0. 1. 0.; 0. 0. 1.])
3×3 SparseMatrixCSC{Float64, Int64} with 3 stored entries:
1.0 ⋅ ⋅
⋅ 1.0 ⋅
⋅ ⋅ 1.0
julia> Matrix(1.0I, 3, 3) #Dense format || Array{Float64}(I,3,3)
3×3 Matrix{Float64}:
1.0 0.0 0.0
0.0 1.0 0.0
0.0 0.0 1.0
julia> sparse(Matrix(1.0I,3,3)) #convert from Dense to Sparse matrix(a n-by-n identity matrix)
3×3 SparseMatrixCSC{Float64, Int64} with 3 stored entries:
1.0 ⋅ ⋅
⋅ 1.0 ⋅
⋅ ⋅ 1.0
julia> A = sparse([1, 1, 2, 3], [1, 3, 2, 3], [0, 1, 2, 0])
#3×3 SparseMatrixCSC{Int64, Int64} with 4 stored entries:
0 ⋅ 1
⋅ 2 ⋅
⋅ ⋅ 0
julia> dropzeros(A) #Removes stored numerical zeros
3×3 SparseMatrixCSC{Int64, Int64} with 2 stored entries:
⋅ ⋅ 1
⋅ 2 ⋅
⋅ ⋅ ⋅
julia> spzeros(ni, nj) #Creates a m-by-n matrix of zeros
3×3 SparseMatrixCSC{Float64, Int64} with 0 stored entries:
⋅ ⋅ ⋅
⋅ ⋅ ⋅
⋅ ⋅ ⋅
julia> a.m # Number of rows
3
julia> a.n # Number of columns
3
julia> a.colptr # Column j is in colptr[j]:(colptr[j+1]-1)
4-element Vector{Int64}:
1
2
3
4
julia> a.rowval # Row indices of stored values
3-element Vector{Int64}:
1
2
3
julia> a.nzval # Stored values, typically nonzeros
3-element Vector{Float64}:
1.0
1.0
1.0Implementation #2: Local AD
更に、同論文では”LocalAD”なる新たな概念を構築し、之までの手法との比較検討の結果はTable 6.1に示されるように、処理速度の格段の向上に寄与する優位性を示している。ただ、同貯留層モデルが利用できないため自分自身で検証できていない。
”LocalAD”法とは対象モデル全体に於ける大規模なヤコビアン行列(偏導関数)を引きずっていくのではなく局所的にヤコビ行列を構築して演算負荷の低減を図るものである。そのためヤコビ行列の構築には多少の処理が必要となる。
In-house Implementation
一方、俺の最初に開発した自家製ADモジュール(“ForwardAD”)は同論文”FowardAutoDiff”と同じく疎行列に基づくprimitiveなものである。同論文で提唱されている”CustomJacobianAutoDiff (CJAD)”モジュールの実装は俺の言語技術能力的に無理であるが、”LocalAD”は解析微分に匹敵する演算速度を達成する蓋然性が高いことから、第二のADモジュール(“LocalAD”)として気合を入魂して導入する。尚、同論文では静的配列(@SVector)を使うことで演算効率の最適化を図っているが、特殊な宣言なので使用に留意を要する上に、俺には実装する技量がない為モジュールには組み込んでいない。
ローゼンブロック関数に適用したニュートン法の自動微分モジュールとして、従来型”ForwardAD”と新型”LocalAD”を紹介の上、偏導関数構築の差異を具体的に比較する。
先ず、従来型”ForwardAD”モジュールに基づく処理事例を見てみる。
function newtonMethodAD(X, tol, itrMax)
for stp_i1 = 1:itrMax
resi = [grad1Rosenbrock(X).val, grad2Rosenbrock(X).val]
grad = Matrix[grad1Rosenbrock(X).der; grad2Rosenbrock(X).der]
r1 = reshape(grad,2,1)[1]; r2 = reshape(grad,2,1)[2]; r3 = vcat(r1,r2)
X = X - r3 \ resi
if norm(resi,2) < tol
return X, resi, grad, stp_i1
end
end
return X, resi, grad, itrMax
end一方、新型”LocalAD”に基づく処理事例を紹介する。
function newtonMethodAD(x, y, tol, itrMax)
for stp_i1 = 1:itrMax
x = variableLAD(double(x), 1); y = variableLAD(double(y), 0)
df1 = [grad1Rosenbrock(x,y).der grad2Rosenbrock(x,y).der] #space
x = variableLAD(double(x), 0); y = variableLAD(double(y), 1)
df2 = [grad1Rosenbrock(x,y).der grad2Rosenbrock(x,y).der] #space
resi = [grad1Rosenbrock(x,y).val, grad2Rosenbrock(x,y).val]
grad = vcat(df1, df2)
x = x - (grad \ resi)[1]
y = y - (grad \ resi)[2]
if norm(resi,2) < tol
return x, y, resi, grad, stp_i1
end
end
return x, y, resi, grad, itrMax
endここで、勾配ベクトル(grad1Rosenbrock()、grad2Rosenbrock())は、Part 2 式(3-7)で示すように、$$\nabla f =\begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix}
=\begin{bmatrix} 2(x-a) – 4bx(y – x^2) \\ 2b(y-x^2) \end{bmatrix}\tag{3-7}$$
2式で与えられので、其々2変数に対する偏導関数を求める必要がある。
これに対して、変数毎に偏導関数を求めるに当たり、関数値を2度求めることを強いられるものの、偏関数の算定は変数毎に適宜指示することで対処する。因みに、下記のようにモジュールに組込んだvariableLAD関数の引数に於いて”1″は偏導関数の算定、”0″は不算定を意味する。
function grad1Rosenbrock(X, a=1., b=100.)
x, y = X
return (2 * (x - a) - 4 * b * x * (y - x^2))
end
function grad2Rosenbrock(X, a=1., b=100.)
x, y = X
return (2 * b * (y - x^2))
end以上、”LocalAD”に基づく偏微分値の算定方法である。
ここで、”ForwardAD”並びに”LocalAD”モジュールに置けるコアな構造体(クラス)宣言部分のコードを紹介しておく。それ以降のコードはオーバーロード若しくは多重定義を用いた演算子関数の集合体から構成される。
”ForwardAD”モジュールから
module ForwardAD
using LinearAlgebra, SparseArrays
export FAD, variableFAD, double, assembleJacobianAD, assembleVariableAD, printFormatAD
import Base: -, +, *, /, ^, exp, sqrt, log, sin, cos, tan
import Base: inv, iterate, getindex, setindex!, == #for test
struct FAD
val
der
end
function variableFAD(argVal, argDer...)
if isempty(argDer)
argIn = (argVal,)
mArg = length(argIn)
argOut = Array{FAD}(undef,mArg)
for i in 1:mArg
der = Array{SparseMatrixCSC{Float64,Int64},1}(undef,mArg)
[der[j] = i == j ? sparse(I, length(argIn[i]), length(argIn[i])) :
spzeros(length(argIn[i]), length(argIn[j]))
for j in 1:mArg]
argOut[i] = FAD(argIn[i],der)
end
argOut[length(argOut)]
else
return (argVal, argDer...)
end
end
+(A::FAD, B::Number) = FAD(A.val + B, A.der)
...次は”LocalAD”モジュール
module LocalAD
export LAD, variableLAD, double, assembleJacobianAD, assembleVariableAD, printFormatAD
import Base: +, -, *, /, ^, sqrt, log, exp, sin, cos, tan
struct LAD
val
der
end
function variableLAD(val, derIndex::Int)
der = derIndex > 0 ? 1 : 0
return LAD(val, der)
end
import Base: +
function +(A::LAD, B::LAD)
return LAD(A.val + B.val, A.der + B.der)
end
...Other Outstanding Issue
ADモジュールの実装を終えた後、貯留層シミュ−レーターに組込むヤコビアン行列の合体を視野に入れ、個々のAD変数を合体して一元化する関数”assembleVariableAD”の実装方法に悩む。
同関数の入力はベクトル入力とスカラー入力の二種類のケースに対応する必要が有る。Python言語ではこれに対して容易く対処する事ができたが、Julia言語では型規定が厳しく明示的に型変換をするも上手く呼び込めない。数日試行錯誤するが、結局、これも多重定義にて解決することができた。
ここで、具体的にコードで違いを比べてみよう。
function assembleVariableAD(adObj) #multiple dispatch (Array version)
# Assemble AD variable-Arrays depending on other independent AD variable-Arrays
allVal = [getfield(ad, :val) for ad in adObj]
allDer = [getfield(ad, :der) for ad in adObj]
return LAD( vcat(allVal), vcat(allDer) )
end
function assembleVariableAD(adObj...) #multiple dispatch (NOT Array version)
# Assemble AD variables depending on other independent AD variables
argIn = [adObj...]
if typeof(argIn)==Vector{LAD}
allVal = [getfield(ad, :val) for ad in argIn]
allDer = [getfield(ad, :der) for ad in argIn]
return LAD( allVal, allDer )
else
error("@Multiple dispatch #2 _assembleVariableAD error encountered.")
end
endClosing
丸4ヶ月に渡る冬籠りの末、何とかPython、Julia言語によるADモジュールの実装を終える。将来的にはGitHubにUploadする予定であるが、果たして、究極的な目標であるiSMARTに実装して上手く効率的にWorkするかどうか自信はなく、その確認を待ってから掲載したい。
新たな展開に向けて気持ちも新たに。
一気にJulia版iSMARTを作成するか。Julia版SMARTSOL(Matrix Solver)を作成するか、又はJuliaからFortranコードを呼込む形式で茶を濁すか。決めかねている。
何れにしてもまだまだ人生を楽しめそうだ!
「紅白で 完成祝う 牡丹かな」





盛春に咲いた椿。品種は紅乙女。何とも云えない色香

Seize the day!
References
- JuliaDiff: Differentiation tools in Julia. JuliaDiff on GitHub
- Julia 1.8 Documentation
- Julia Cheat Sheet for v 1.0
- The Julia Programming Language: Frequently Asked Questions
- Sindre Grøstad, June 2019. Automatic Differentiation in Julia with Applications to Numerical Solution of PDEs. Master’s thesis in Applied Physics and Mathematics, NTNU
以上
Appendix: Julia Language Profile
この機会に、俺的なJulia言語の主要な論点について取り纏める。長文となるが、ご了承賜りたい。
JuliaはMathematicianが構築した言語だけあって数学的な見識が随所に根付いている。数式で表記できることは美しいが、俺は自動微分で利用する事が有るため多用する気はない。一方、Pythonはプログラマーが創始者の為かごちゃごちゃあって紛らわしく、物覚えの悪い俺には順応し難い。特に、if name == ‘main’、all、init等の表記も不自然で気に食わない。
俺的な学んだ中で主だったGistを以下に整理しておく。
- 行列・ベクトルに対する明快な取決め・姿勢が伺える。科学技術計算でよく使われるベクトル、行列の取扱い方については多岐にわたるので留意しておく。尤も、Fortranでは配列表記は”()”の形式しかなくより覚えやすい。Juliaで最も気に入ったのは、Fortran同様、配列要素の順序が”0”ではなく”1”から始まること。俺は未だに”0”開始には慣れない。
- 多重定義(Multiple Dispatch)は引数の型が違う関数は名前が同じでも別の定義として宣言できる。C++のメンバ関数呼び出しに当たるもので是非おさえておきたい
- 線形計算の求解と除算を混同しないこと
- Broadcastも秀でた特徴。重宝する
- 最低限のsyntaxは覚えておく。俺なりにAD実装に役立ったものを後述する
- マクロ表記も便利。特に、Test、Benchmark、Profile、Timeは有益
各々の論点につき事例を交えながら俺的なポイントを以下に整理する。
Array
配列に関する具体的な取決めはJuliaHubの”Vectors and matrices”が有益。一度は目を通しておくべき。
- [x,y,z] calls vect and creates a 1-dimensional array
- [x; y; z] calls vcat to vertically concatenate values together. …
- [x y z] calls hcat to horizontally concatenate values together. …
- finally [w x; y z] calls hvcat to horizontally and vertically concatenate values together to create a container in two dimensions….
1D Array (Vector)
要は、一次元配列は列ベクトル(Element/Column Vector)として扱われ、ベクトルは原則列ベクトルと定義される(この方が行列計算では自然だ)。コロン”,”、セミコロン”;”で区切ると列ベクトルになり、空白(␣)で数値を区切ると行ベクトル(Row Vector)になる。列ベクトルを行ベクトルに変換するにはreshapeを用いる。配列要素の順番はFortran同様、列優位(column-major order型)でポインタ渡しである。
一次配列を構築する場合の特記事項及び事例につき見ていこう。
julia> [1, 2, 3] #column vector
3-element Vector{Int64}:
1
2
3
julia> [1; 2; 3] #column vector
3-element Vector{Int64}:
1
2
3
julia> [1改行
2改行
3] #column vector
3-element Vector{Int64}:
1
2
3
julia> [1␣2␣3] #row vector
1×3 Matrix{Int64}:
1 2 3
julia> reshape([1, 2, 3], 1, 3) #convert form column to row vector
1×3 Matrix{Int64}:
1 2 3
julia> [1 2; 3 4]
2×2 Matrix{Int64}:
1 2
3 4Matrix(行列)、Vector(ベクトル)の上位にAbstractArrayと称する抽象配列が位置する。Fig.1 Abstract Array Type Treeを参照のこと。
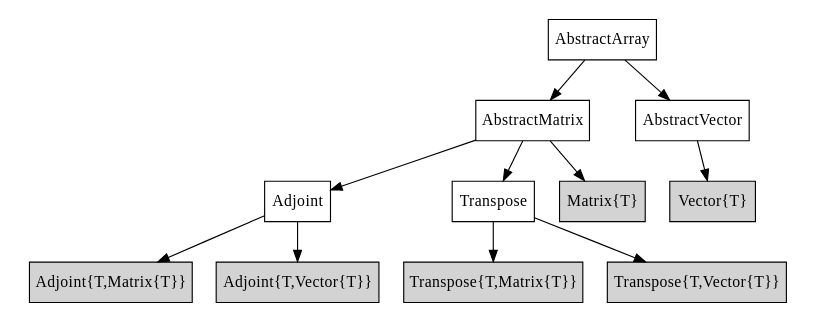
Array Constructor
配列はArray{T}(undef, dims…)で定義する。一次元配列はArray{T,1}、2次元配列はArray{T,2}、三次元配列はArray{T,3}と表記。TはTypeの事。zeros、ones等初期化も同様の表記で構築できる。
julia> Array{Type}(undef,m) #|| Array{Type,1}(undef,m)
julia> Vector{Type}(undef,m) #||
julia> Array{Float64,1}(undef,3) #instance float64 1D array. values may not be initialzed by zero!
3-element Vector{Float64}:
0.0
6.9448778755838e-310
6.9448778755877e-310
julia> Array{Float64,2}(undef,3,2) #instance float64 2D array. values may not be initialzed by zero!
3×2 Matrix{Float64}:
0.0 0.0
6.94487e-310 6.94487e-310
6.94487e-310 6.94487e-310
julia> Array{Float64,3}(undef,3,2,2) #instance float64 3D array. values are not initialzed by zero!
3×2×2 Array{Float64, 3}:
[:, :, 1] =
0.0 0.0
6.94487e-310 6.94487e-310
6.94487e-310 6.94487e-310
[:, :, 2] =
0.0 0.0
6.94487e-310 6.94487e-310
6.94487e-310 6.94487e-310Others related to Array
その他の行列に関わる重要なポイント
- 配列の要素は全て同じ型である
小数点を明示的に表記することで自動でFloat64(倍精度)と解釈する。明示ない場合Int64となる - タプル(Tuple)変数をベクトル(Vector)に変換するには”collect”を用いる
変数や数値をカンマで区切って単に複数並べたものをTupleと呼ぶが、 要素の型はどうでも良い。しかし、collectでベクトルに変換する場合には同じ型でなければ受け付けてくれない - 配列の要素を定義する場合、範囲、式、やループを利用できる
- 配列syntax要素を変更する場合、syntaxの最後に”!”を付加する
- 二次元配列構築に於いて、列は空白”␣”、行は改行乃至はセミコロン”;”で区切る
- ベクトルの要素同士の演算は演算子の前にドット”.”を付ける
- 行列Aの転置行列をA’で示すことも可能。通常は関数transpose(A) で表記する
- 内積計算には”*”乃至はdot関数を用いる
- 配列のコピー(copy)の取扱いには注意を要する
参照コピーでは無く単純な値のコピーとなる。故に、\(c = copy(a)\)とすると、\(a\)のコピーが新しく作られて\(c\)とする。\(a\)と\(c\)は要素の中身が偶々同じだが別変数が作成される。\(a\)と\(c\)のポインタは異なる。一方、\(b = a\)とすると\(b\)の実体が\(a\)の実体そのものを指す。名前が違うだけで実体は1つなので、\(a\)の要素を変更すると同時に\(b\)の要素も変更される。又、\(a\)と\(b\)のポインタはIdenticalである。
julia> t = -0.5,4.0 #tuple
(-0.5, 4.0)
julia> a = collect(t) #conver to column vector
2-element Vector{Float64}:
-0.5
4.0
julia> a = [1 2
3 4]
2×2 Matrix{Int64}:
1 2
3 4
julia> a[:,:]
2×2 Matrix{Int64}:
1 2
3 4
julia> a[1,:]
2-element Vector{Int64}:
1
2
julia> a[:,1]
2-element Vector{Int64}:
1
3
julia> a[begin:end,begin:end]
2×2 Matrix{Int64}:
1 2
3 4
julia> getindex(a,1,2) #find element at index @(1,2)
2
julia> setindex!(a,-1,3) #reset value:-1 at index @4 (count by element-wise)
2×2 Matrix{Int64}:
1 -1
3 4
julia> a = [1 2;3 4]
2×2 Matrix{Int64}:
1 2
3 4
julia> a' #transpose
2×2 adjoint(::Matrix{Int64}) with eltype Int64:
1 3
2 4
julia> [1 2; 3 4]' #transpose
2×2 adjoint(::Matrix{Int64}) with eltype Int64:
1 3
2 4
julia> b = [1␣2] #row vector
1×2 Matrix{Int64}:
1 2
julia> a .* b #multiply by element wise
2×2 Matrix{Int64}:
1 4
3 8
julia> a * b #multiply matrix by matrix
ERROR: DimensionMismatch: arguments must have the same number of rows
julia> b .* b #multiply by element-wise
1×2 Matrix{Int64}:
1 4
julia> dot(b,b) #inner product
5
julia> c = reshape(b,2,1) #convert 1×2 Matrix to 2×1 Matrix
2×1 Matrix{Int64}:
1
2
julia> b * c #multiply by matrix -> inner product
1×1 Matrix{Int64}:
5
julia> sin(a) #sin by matrix
2×2 Matrix{Float64}:
-0.465581 -0.148424
-0.222637 -0.688218
julia> sin.(a) #sin by elementary-wise
2×2 Matrix{Float64}:
0.841471 -0.841471
0.14112 -0.756802
julia> a
2×2 Matrix{Int64}:
1 2
3 4
julia> b = a
2×2 Matrix{Int64}:
1 2
3 4
julia> c = copy(a)
2×2 Matrix{Int64}:
1 2
3 4
julia> a[1,1] = 0
0
julia> a
2×2 Matrix{Int64}:
0 2
3 4
julia> b
2×2 Matrix{Int64}:
0 2
3 4
julia> pointer(a) #pointer of a
Ptr{Int64} @0x00007fe9f22449a0
julia> pointer(b)
Ptr{Int64} @0x00007fe9f22449a0 #pointer of b == pointer of a
julia> pointer(c)
Ptr{Int64} @0x00007fe9f269a560その他配列絡みのsyntax
julia> a = Vector(1:0.5:2) #initialize array by range == Array(1:0.5:2)
3-element Vector{Float64}:
1.0
1.5
2.0
julia> zeros(Float64,3,2,1) #initialize 3D array by zero
3×2×1 Array{Float64, 3}:
[:, :, 1] =
0.0 0.0
0.0 0.0
0.0 0.0
julia> ones(Float64,3,2) #initialize 3D array by one
3×2 Matrix{Float64}:
1.0 1.0
1.0 1.0
1.0 1.0
julia> fill(1.0, 3,2) #Create an array of size dims set to value
3×2 Matrix{Float64}:
1.0 1.0
1.0 1.0
1.0 1.0
julia> vcat(A...) #sparse_vcat(A...)
julia> vcat(a,a) #append vertically
4×2 Matrix{Int64}:
1 2
3 4
1 2
3 4
julia> hcat(A...) #sparse_hcat(A...)
julia> hcat(a,a) #append horizontally
2×4 Matrix{Int64}:
1 2 1 2
3 4 3 4
julia> maximum(a) #max of a's element
4
julia> minimum(a) #min of a's element
1
julia> extrema(a) #min & max of a's element
(1, 4)
julia> using LinearAlgebra #should be declared
julia> Array{Float64}(I,3,3) #initialize by Identity matrix
3×3 Matrix{Float64}:
1.0 0.0 0.0
0.0 1.0 0.0
0.0 0.0 1.0
julia> diag(a) #display diag element
2-element Vector{Int64}:
1
4
julia> Diagonal(a) #display diagonal array
2×2 Diagonal{Int64, Vector{Int64}}:
1 ⋅
⋅ 4
julia> ndims(a) #find number of dimension
2
julia> length(a) #find number of toal elements
4
julia> a[:,:,:] #add one dimension
2×2×1 Array{Int64, 3}:
[:, :, 1] =
1 2
3 4Interface
ADモジュールでは下記syntaxに対してAD変数を多重している。
- iterate(iter, state): 次の項目と次の状態のタプルか、項目が残っていない場合は nothingを返す
- getindex(X, ix): X[ix] インデックス付きエレメントアクセス
- setindex!(X, v, ix): X[ix]=v、インデックス付き割り当て
function iterate(iter::FAD, state = 1)
if state > length(iter.val)
return nothing
end
return (iter[state], state + 1)
endBroadcast
- サイズの異なる配列同士の演算が可能
julia> a
2×2 Matrix{Int64}:
1 2
3 4
julia> b = [1 2]
1×2 Matrix{Int64}:
1 2
julia> broadcast(+,a,b)
2×2 Matrix{Int64}:
2 4
4 6
julia> a .+ b
2×2 Matrix{Int64}:
2 4
4 6- 関数呼び出しは,ドット構文”.”を用いてベクトル化して、配列や複雑な存在の要素其々に対して同じ関数を作用させれる。
- @.構文はそれ以降の数式全体にブロードキャストを適用する。
julia> a = [1 2; 3 4]
2×2 Matrix{Int64}:
1 2
3 4
julia> map(x -> 2x, a) "broadcast to map function
2×2 Matrix{Int64}:
2 4
6 8
julia> exp.([1., 2., 3.])
3-element Vector{Float64}:
2.718281828459045
7.38905609893065
20.085536923187668
julia> x = rand(3)
3-element Vector{Float64}:
0.7914289957457029
0.3167245428227382
0.030360692693636726
julia> @. x^2 + 2x + 1 "broadcast @. macro
3-element Vector{Float64}:
3.209217846798458
1.733763521671749
1.0616431570481109Left(/) or Right Division(\)
連立一次方程式\(Ax = b\) の解(x)を求める演算子(\)が用意されている(\(A\times {b^{-1}}\))。一般的な除算(A/b)とは混同しないこと
julia> a
2×2 Matrix{Int64}:
1 2
3 4
julia> b
1×2 Matrix{Int64}:
1 2
julia> a ./ b #divide by element-wise
2×2 Matrix{Float64}:
1.0 1.0
3.0 2.0
julia> x = a .\ b #solve ax = b && divide by element-wise
2×2 Matrix{Float64}:
1.0 1.0
0.333333 0.5
julia> x = a \ b #solve ax = b
ERROR: DimensionMismatch: arguments must have the same number of rows
julia> a
2×2 Matrix{Int64}:
1 2
3 4
julia> b = [1, 2]
2-element Vector{Int64}:
1
2
julia> a ./ b #divide by element-wise
2×2 Matrix{Float64}:
1.0 2.0
1.5 2.0
julia> x = a .\ b #solve ax = b && divide by element-wise
2×2 Matrix{Float64}:
1.0 0.5
0.666667 0.5
julia> x = a .\ reshape(b,1,2)
2×2 Matrix{Float64}:
1.0 1.0
0.333333 0.5
julia> x = a \ b #solve ax = b
2-element Vector{Float64}:
0.0
0.5Overall Julia
Julia言語全体に関する重要なポイント。一部Julia Documentより引用している。
- JuliaのnothingはPythonのNoneに相当する
- 変数・数値の型はtypeof関数で確認する
- 無名関数(anonymous function)はmap関数等で有益: 引数 -> 出力式(関数)
- 二変数以上の関数値を返す方法
- 関数引数を可変長引数として宣言するには、仮引数に”…”を付加する
- 関数引数は明示的に型宣言可。又、関数値の型に制約をつけるには関数名()の後に::型をつける
- isa関数はPythonのisinstanceと同等に使える。isempty関数も有用
julia> typeof(nothing)
Nothing
julia> typeof(a) #find type
Matrix{Int64} (alias for Array{Int64, 2})
julia> x -> x^2 + 2x - 1 #anonymous function: == function(x) = x^2 + 2x - 1
#1 (generic function with 1 method)
julia> map(x -> x^2 + 2x - 1, [1.,3.,-1.]) #useful for map function: x = [1.,3.,-1.]
3-element Vector{Float64}:
2.0
14.0
-2.0
julia> function (x::Float64) #define argument-type
x^2 + 2x - 1
end
#1 (generic function with 1 method)
julia> function f(x::Float64)::Float64 #define return type
end
f (generic function with 2 methods)
julia> function foo(a,b) #returning more than one variable
return a+b, a*b
end
foo (generic function with 1 method)
julia> bar(a,b,x...) = (a,b,x) #variable number of arguments: 3+
bar (generic function with 1 method)
julia> bar(1,2,3) #variable number of arguments: 3
(1, 2, (3,))
julia> bar(1, 2, 3, 4) #variable number of arguments: 4
(1, 2, (3, 4)) # 2 + one tuple (2)
julia> x = [3,4] #vector od 2 elements
2-element Array{Int64,1}:
3
4
julia> bar(1,2,x...) # 2 + one tuple (2)
(1, 2, (3, 4))
julia> isa(1.0, Int) #like isinstance in Python
false
julia> isa(Inf, Float64) #syntax:Inf
true
julia> isnothing(a) #syntax:isnothing
false
julia> isempty #syntax:isempty
false
julia> zip(bar,x) #tuple of values of its subiterators
zip((1, 2, (3, 4)), [3, 4])Built-in Macro
コマンドや式が実際にどのような動作しているのか見るには、コマンドの前に@code_loweredをつけて実行する。
デバッグ用@show @assert @testやPerformanceチェック用@time @benchmark @profiler @profileviewが有益。一部事例をご紹介
julia> m = randn(2,2)
2×2 Matrix{Float64}:
-1.17015 -0.281928
0.247229 0.753965
julia> v = randn(2)
2-element Vector{Float64}:
-0.6822660597240726
0.19859284033102756
julia> @time m * v
0.000015 seconds (1 allocation: 80 bytes)
2-element Vector{Float64}:
0.7423622432902717
-0.01894369984654759
julia> @benchmark m * v
BenchmarkTools.Trial: 10000 samples with 911 evaluations.
Range (min … max): 118.530 ns … 3.364 μs ┊ GC (min … max): 0.00% … 96.01%
Time (median): 121.145 ns ┊ GC (median): 0.00%
Time (mean ± σ): 133.004 ns ± 120.911 ns ┊ GC (mean ± σ): 3.57% ± 3.81%
▆█▃ ▃▃▂▂▁ ▁ ▁▃▁ ▁
█████████████████████▇██▆▆▅▆▆▆▅▅▅▅▅▄▅▅▃▃▄▃▄▄▅▅▅▄▃▄▄▄▃▄▅▃▄▂▄▄▄ █
119 ns Histogram: log(frequency) by time 234 ns <
Memory estimate: 80 bytes, allocs estimate: 1.Machine Epsilon
Machine Epsilonが標準で組込まれている。感動もの!
julia> eps(Float64)
2.220446049250313e-16
julia> eps(1.0)
2.220446049250313e-16openAI
chatGPTの衝撃的デビューは産業革命以降の最大のパラダイムシフトのきっかけとして前向きに捉えている。人類にとってはさらなる進化に向けて大きく成長すると信じている。
chatGPTは未だ使ったことはないのだが、Julia言語には慣れていない俺にとっては家庭教師の役割を期待し喜ばしいシステムと歓迎したい。OpenAIとの連携でJuliaのコーディング能力が一段と向上するのは間違いない。Freeで使い放題利用できるシステムが来る日を待とう。
〆