iSMART〜Automatic Differentiation Part 2
Pythonによる自動微分クラスの構築、実装の検証編をお届けします。単なるプログラミングな知見を駆使するだけで自動微分の肝はPart 1に集約されます。Part 2 would hopefully address an implementation and verification of the Automatic Differentiation Initiative class in Python. A mere programming skill is required in this part. The core of AD could be covered in Part 1.
AD Mode
自動微分にはフォーワード型(Forward型)とリバース型(Reverse型)の2種類ある。どちらも微分の連鎖律を用いて関数を単純な演算に分解して導関数値を求める方法であるが分解の仕方が異なる。
Forward型では一つの入力変数に対して全ての中間変数の導関数値を同時に順(順伝播)に演算していく手法で、関数値と同時に導関数値を算定することができる利点がある。算定順序は下式の導関数の連鎖律で示される。
以下、Wikipedia自動微分より引用。
$$\frac{\partial y}{\partial x}= \frac{\partial y}{\partial w_1} \frac{\partial w_1}{\partial x}
= \frac{\partial y}{\partial w_1} \left(\frac{\partial w_1}{\partial w_2} \frac{\partial w_2}{\partial x}\right)
= \frac{\partial y}{\partial w_1} \left(\frac{\partial w_1}{\partial w_2} \left(\frac{\partial w_2}{\partial w_3} \frac{\partial w_3}{\partial x}\right)\right)= \cdots \tag{1-1}$$
一方、Reverse型では一つの出力変数について全ての中間変数に対する偏導関数値を演算していく手法。一度算定した後、各中間変数が算定された履歴を逆向き(逆伝播)に辿って導関数値を算定する為、算定履歴(グラフ)を保存するための記憶容量が必要となる。
この場合の算定順序は次の導関数の連鎖律で与えられる。
$$\frac{\partial y}{\partial x}= \frac{\partial y}{\partial w_1} \frac{\partial w_1}{\partial x}
= \left(\frac{\partial y}{\partial w_2} \frac{\partial w_2}{\partial w_1}\right) \frac{\partial w_1}{\partial x}
= \left(\left(\frac{\partial y}{\partial w_3} \frac{\partial w_3}{\partial w_2}\right) \frac{\partial w_2}{\partial w_1}\right) \frac{\partial w_1}{\partial x}= \cdots \tag{1-2}$$
一般的に、入力変数の方が多いときはReverse型、出力変数の方が多い時はForward型を使うのが計算量の点で有利になる。ニューラルネットワークのバックプロパゲーションはReverse型の一種である。
石油上流業界で使われる貯留層シミュレーターの分野では出力変数の方が多い故、Forward型が一般的であるようだ。
Implementation
実装の方法は大きく分けてソースコードの変換とオペレータオーバーローディングによる方法の2種類の方法がある。前回述べたようにオペレータオーバーロードによる実装が比較的容易なのでこれを採用する。
今回Python言語を用いて特殊メソッドによる演算子を組込むADクラスを構築する。具体的に構築したクラス(Object Class)名をFAD(Forward Automatic Differentiation Initiative)と定める。宣言する変数は、ベクトル(vector)と一階偏微分行列(derivative)から構成されるインスタンスである。
\(m\)次元関数\(n\)独立変数(\(f:\mathbb {R^{n}} \to \mathbb{R^{m}}\))で構成されるヤコビ行列
$$J=\frac{\partial \mathbf{f}}{\partial \mathbf{x}}=\begin{bmatrix} \frac{\partial f_{1}}{\partial x_{1}} & \ldots & \frac{\partial f_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}} & \ldots & \frac{\partial f_{m}}{\partial x_{n}} \end{bmatrix}\tag{2}$$
に対して繰り返しになるが、変数\(\mathbf{x}\)は関数値はベクトル、偏微分値は行列(対角)のペアで構成される。言い換えれば、変数\(x\)の値は\(x.val\)、偏微分の値は\(x.der\)で呼び出せる。偏微分値のDefaultは”1”であるが、任意に与えることも可能である。例えば、3変数\(x\)の値を\(1,2,3\)とすると、Default設定では下記のように配列で構成される。
$$\mathbf{x} = \begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix} = \left( \begin{array}{c|ccc} val &&der \\1 &1 &0 &0 \\2 &0 &1 &0 \\3 &0 &0 &1\end{array} \right)$$
クラス構築に当たってのポイントは以下の通り。
- 同クラスの入力変数はベクトル(Vector)を想定しているが、単一の数値の入力も可能。一方、偏導関数(derivative)は対角行列であるのでメモリ効率の観点から行列要素の格納方法に留意すべきである。C++/Pythonは行優位故CSR(圧縮行格納)、Fortran/Juliaは列優位故CSC(圧縮列格納)が適切となろうが、JuliaはSparseMatrixCSC関数がデフォルトでCRC関数はないようだ。因みに、資料7はこの点に関連した演算速度の検証を行っているが、俺はそこまで凝る必要なく単純に解析微分を盛り込む方がHealthyであろう。従って、フル行列として格納している現コードを変更する気はない。速度的にはベクトル入力は避けて単一の数値入力が最も有利かもしれない。
- クラス内で演算子の特殊メソッドを組込む
- 全体ヤコビアンに対して小ヤコビアン(Sub Jacobian)を適宜追加する機能を組込む。本機能は貯留層シミューレーターに於いて残差方程式の追加に対応するヤコビアンの組込みを睨んだ機能である。具体的には、vcatJacAD、joinJacADの2関数を組込む
- 行列の内積の演算子dot関数を組込む(通常Numpy.dot機能を使うだろう)。その他の行列計算は基本的に要素毎の演算である。Julia言語では要素同士の演算は演算子の前に明示的にドット” .”を付ける。
class FAD(object):
"""
FAD.py: Python Forward Automatic Differentiation Initiative (FAD) Core Module
...
studioPaGoNa
"""
def __init__(self, val=None, der=None): #*args):
if val is None:
self.val = []
self.der = []
elif der is None:
self.val = val
try:
val[0]
except:
self.der = 1
else:
self.der = np.eye(len(val))
else:
self.val = val
self.der = derVerification of AD Class
検証用の課題として下記資料[2]、[3]から夫々下二題を選出して実装を検証する。
1. Univariate Application: \(f (x) = e^{-\sqrt{x}} \sin(x\log(1 + x^{2}))\)
減衰振動関数がゼロになる値をニュートン法によって求める課題
def funcUnivariate(X):
x = FAD(X)
y = exp(-sqrt(x))*sin(x*log(1 + x**2))
return y.double()
def newtonFuncUnivariate(X):
dX = 1.
while abs(dX) > 1.0e-6:
fAD = funcUnivariate(X)
dX = fAD[0] / fAD[1]
X = X - dX
return X
X_ini = 5.
print('\nX_ini =',X_ini,'-> X* =',newtonFuncUnivariate(X_ini))root_ini = 5.0 -> root* = 4.88705596745554252. Example A.5.4 Minimizing the Rosenbrock equation
ローゼンブロック関数とは、最適化問題としてよく用いられるベンチマーク関数で、次式で定義される。
$$f(x,y) = (a-x)^2 + b(y-x^2)^2\tag{3-1}$$
因みに、同関数の多変量関数は次式で与えられる。
$$f(x) = f(x_1,x_2,x_3,…,x_n) = \sum_{i=1}^{N/2} [100(x_{2i-1}^2 – x_{2i})^2 + (x_{2i-1}-1)^2]\tag{3-2}$$
上式に於いて\(f(x,y)=0\)なる時の最小値(Global Minimum)は\((x,y)=(a,a^{2})\)であることは良く知られている。
ローゼンブロック関数は、1960年にハワード ローゼンブロックが発表した非凸関数で極小値(Local Minimum)は見つけることは難しくはないが、最小値(Global Minimum)は細長い放物線状の平坦な谷の中にある為、最小値に収束させることが困難な課題である。このためローゼンブロックの谷、ローゼンブロックのバナナ関数とも呼ばれる。
ここで最も高速な方法として知られるニュートン法にて解を求めよう。ニュートン法はニュートン・ラプソン法とも呼ばれ、非線形代数方程式や非線形最小問題の解法として幅広く用いられている。
最小化問題に於ける関数\(f:\mathbb {R} \to \mathbb{R}\)に対し、任意の初期値\(\mathbf{x}_k\in \mathbb{R}\)にて\(f(\mathbf{x})\)をテイラー展開して二次多項式に近似する。
$$f(\mathbf{x}) \simeq f(\mathbf{x _ k}) + \nabla f(\mathbf{x} _ k)^\mathrm{T} (\mathbf{x} – \mathbf{x} _ k) + \frac{1}{2} (\mathbf{x} – \mathbf{x} _ k) ^ \mathrm{T} \nabla ^ 2 f(\mathbf{x} _ k)(\mathbf{x} – \mathbf{x} _ k)\tag{3-3}$$
その二次多項式の局所最適解のある方向を探索することで、より早く真の最適解に近づけると考える。ここで目的関数\(f(\mathbf{x})\)は二回連続微分可能であり、一階偏微分係数と二階偏微分係数が継続的に\(0\)になる領域を持たないものとする。
もし\(\nabla^{2} f(\mathbf{x}_{k})\)が正定値行列であるならば近似式は凸関数となって解は一意に決まる。勾配ベクトルが\(0\)になってこれ以上小さくならない点を局所的最適解と見做すので、\(\mathbf{x}_{k} -(\nabla^{2} f(\mathbf{x}_{k}) )^{-1} \nabla f(\mathbf{x}_{k})\)が停留点となる。
よって、$$\mathbf{x}_{k+1} = \mathbf{x}_{k}-(\nabla^{2} f(\mathbf{x}_{k}) )^{-1} \nabla f(\mathbf{x}_{k})\tag{3-4}$$
を探索方向として用い、\(\mathbf{x}\)を逐次的に更新して真の最適解\(\mathbf{x}^{*}\)に近づいていくアルゴリズムである。
一階偏微分\(\nabla f(\mathbf{x})\)を勾配ベクトル(Gradient)、二階偏微分\(\nabla^{2} f(\mathbf{x})\)をヘッセ行列(Hessian)と呼び、ニュートン法は、正確には二階偏導関数迄用いた先に求めた探索式
$$\mathbf{x_{n+1}} = \mathbf{x_{n}} – \frac{f^{\prime}(\mathbf{x_{n}})}{f^{\prime\prime}(\mathbf{x_{n}})}\tag{3-5}$$
を用いるが、ヘッセ行列の逆行列の算定は演算負荷が更に高くなる為、収束性は劣るものの一階偏導関数による簡素化した探索式を以って代用することが多い。貯留層シミュレーションに於いても一階偏導関数のみで求解を得ている。貯留層シミュレーションに於ける圧力方程式は楕円型が支配的であるが、飽和方程式は局所勾配が急な双曲線型挙動を示すことから非線形性が緩やかなことからこれで充分なようである。
$$\mathbf{x_{n+1}} = \mathbf{x_{n}} – \frac{f(\mathbf{x_{n}})}{f^{\prime}(\mathbf{x_{n}})}\tag{3-6}$$
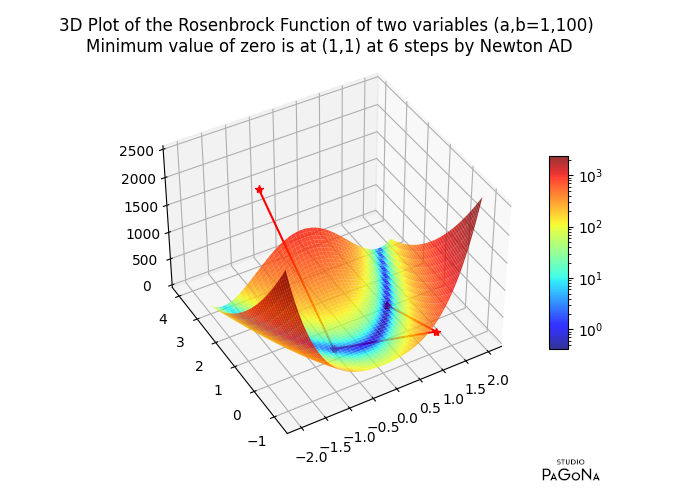
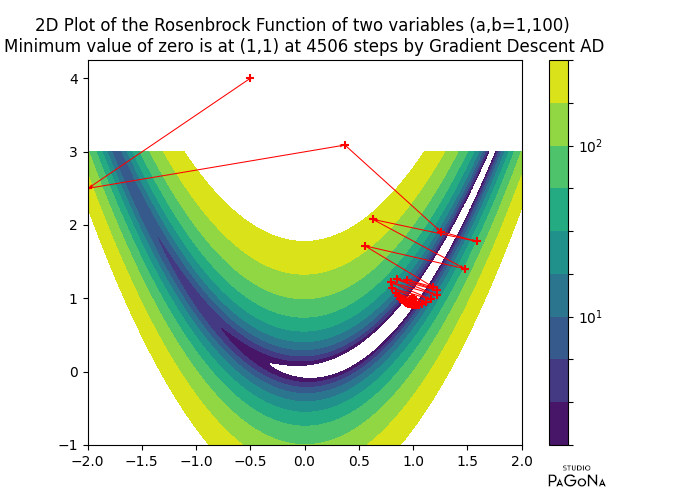
実際、本課題はNon-Convex関数のため一階偏導関数のみによるニュートン法では発散して収束しない。二階偏導関数を使うと反復計算5回で収束する。因みに、最急降下法(Gradient Descent)では反復計算4505回で最適解を得る。

因みに、ローゼンブロック関数に於ける解析偏導関数は以下で与えられる。
勾配ベクトル:
$$\nabla f =\begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix}
=\begin{bmatrix} 2(x-a) – 4bx(y – x^2) \\ 2b(y-x^2) \end{bmatrix}\tag{3-7}$$
今回、ADIクラスには二階偏導関数の自動微分機能を盛り込んでいないので、代替として一階偏導関数解析式(3-7)に対して自動微分にて二階偏微分値を求め、これに対してニュートン法を適用している。この場合、式(3-7)が\(\begin{bmatrix} 0 \\ 0 \end{bmatrix}\)になる時点を収束と見做す。
ヘッセ行列:
$$\nabla^{2} f =\begin{bmatrix} \frac{\partial ^{2}f}{\partial x^{2}} \frac{\partial ^{2}f}{\partial x \partial y} \\ \frac{\partial ^{2}f}{\partial y \partial x} \frac{\partial ^{2}f}{\partial y^{2}} \end{bmatrix}
=\begin{bmatrix} 2-4b(y – 3x^{2}) & -4bx \\ -4bx & 2b \end{bmatrix}\tag{3-8}$$
具体的なPythonコードを下記に引用する。
def funcRosenbrock(X, a=1., b=100.):
x, y = X
return (a - x)**2 + b * (y - x**2)**2
def gradRosenbrock(X, a=1., b=100.):
x, y = X
return np.array([2 * (x - a) - 4 * b * x * (y - x**2),
2 * b * (y - x**2)])
def hessRosenbrock(X, a=1., b=100.):
x, y = X
return np.array([ #np.matrix([
[2 - 4 * b * (y - 3 * x**2), -4 * b * x],
[ -4 * b * x, 2 * b]])
def newtonRapsonMethod(Jacobian, Hessian, x, tol=1e-6, itrMax=1000):
for i in range(1,itrMax):
invHess = np.linalg.inv(Hessian(x))
x = x - np.dot(invHess,Jacobian(x))
#x = x - np.linalg.solve(Hessian(x), Jacobian(x))
if np.linalg.norm(Jacobian(x)) < tol:
return x, i
return x, itrMax
def newtonMethod(Jacobian, x, tol=1e-6, itrMax=1000):
for i in range(1,itrMax):
x = x - Jacobian(x) / funcRosenbrock(x)
if np.linalg.norm(Jacobian(x)) < tol:
return x, i
return x, itrMax
def gradientDescentMethod(Jacobian, x, alpha=0.01, tol=1e-6, itrMax=1000):
for i in range(1,itrMax):
x = x - alpha * Jacobian(x)
if np.linalg.norm(funcRosenbrock(x)) < tol:
return x, i
return x, itrMax
#Global minimum is (x,y)=(a,a^2) for f(x,y)=0
x_ini = [-0.5, 4.0] #np.zeros(2)
x_min, itr = newtonRapsonMethod(gradRosenbrock, hessRosenbrock, x_ini)
print('\nNewton Rapson Method by Analytical Differentiation: Global minimum is (x,y)=(a,a^2) for f(x,y)=0')
print('a =', 1,', b =',100,', x0 =',x_ini,'-> x* =', x_min,'@itr =',itr)
print('@Rosenbrock(x*) =', funcRosenbrock(x_min),', Gradient Rosenbrock(x*) =', gradRosenbrock(x_min))
#Global minimum is (x,y)=(a,a^2) for f(x,y)=0
x_min, itr = newtonMethod(gradRosenbrock, x_ini, itrMax=1000)
print('\nNewton Method by Analytical Differentiation: Global minimum is (x,y)=(a,a^2) for f(x,y)=0')
print('a =', 1,', b =',100,', x0 =',x_ini,'-> x* =', x_min,'@itr =',itr)
print('@Rosenbrock(x*) =', funcRosenbrock(x_min),', Gradient Rosenbrock(x*) =', gradRosenbrock(x_min))
#Global minimum is (x,y)=(a,a^2) for f(x,y)=0
x_min, itr = gradientDescentMethod(gradRosenbrock, x_ini, alpha=0.002, itrMax=5000)
print('\nGradient Descent Method by Analytical Differentiation: Global minimum is (x,y)=(a,a^2) for f(x,y)=0')
print('a =', 1,', b =',100,', x0 =',x_ini,'-> x* =', x_min,'@itr =',itr)
print('@Rosenbrock(x*) =', funcRosenbrock(x_min),', Gradient Rosenbrock(x*) =', gradRosenbrock(x_min))
def grad1Rosenbrock(X, a=1., b=100.):
x, y = X
return (2 * (x - a) - 4 * b * x * (y - x**2))
def grad2Rosenbrock(X, a=1., b=100.):
x, y = X
return (2 * b * (y - x**2))
def newtonMethodAD(X, tol=1e-6, itrMax=1000):
stp_x1, stp_y1 = X.val
for stp_i1 in range(1,itrMax):
resi = np.array([grad1Rosenbrock(X).val, grad2Rosenbrock(X).val])
grad = np.array([grad1Rosenbrock(X).der, grad2Rosenbrock(X).der])
gradInv = np.linalg.inv(grad)
X = X - dot(gradInv, resi) #np.dot(gradInv, resi)
dx, dy = X.val; stp_x1 = np.append(dx, stp_x1); stp_y1 = np.append(dy, stp_y1)
if np.linalg.norm(resi) < tol:
return X, resi, grad, stp_x1, stp_y1, stp_i1
return X, resi, grad, stp_x1, stp_y1, itrMax
resi = np.inf
z = FAD(np.array([-0.5,4.0]))
x_min, resi, grad, stp_x1, stp_y1, stp_i1 = newtonMethodAD(z)
print('a =', 1,', b =',100,', x0 =',x_ini,'-> x* =', x_min.val,'@itr =',stp_i1)
print("@Rosenbrock Gradient (x*) = ", resi)
print("@Rosenbrock AD Hessian(x*) = ", grad)
print('\nGradient Descent Method by Automatic Differentiation')
def gradientDescentMethodAD(X, alpha=0.002, tol=1e-6, itrMax=5000):
stp_x2, stp_y2 = X.val
for stp_i2 in range(1,itrMax):
resi = np.array(funcRosenbrock(X).val)
grad = np.array(funcRosenbrock(X).der)
X = X - alpha * grad
dx, dy = X.val; stp_x2 = np.append(dx, stp_x2); stp_y2 = np.append(dy, stp_y2)
if np.linalg.norm(resi) < tol:
return X, resi, grad, stp_x2, stp_y2, stp_i2
return X, resi, grad, stp_x2, stp_y2, itrMax
resi = np.inf
z = FAD(np.array([-0.5,4.0]))
x_min, resi, grad, stp_x2, stp_y2, stp_i2 = gradientDescentMethodAD(z)
print('a =', 1,', b =',100,', x0 =',x_ini,'-> x* =', x_min.val,'@itr =',stp_i2)
print("@Rosenbrock Function (x*) = ", resi)
print("@Rosenbrock AD Gradient(x*) = ", grad)計算結果はこちら。
Newton Rapson Method by Analytical Differentiation: Global minimum is (x,y)=(a,a^2) for f(x,y)=0
a = 1 , b = 100 , x0 = [-0.5, 4.0] -> x* = [1. 1.] @itr = 5
@Rosenbrock(x*) = 1.4298103907130839e-30 , Gradient Rosenbrock(x*) = [ 4.35207426e-14 -2.22044605e-14]
Newton Method by Analytical Differentiation: Global minimum is (x,y)=(a,a^2) for f(x,y)=0
a = 1 , b = 100 , x0 = [-0.5, 4.0] -> x* = [-8.81974213 21.3638274 ] @itr = 1000
@Rosenbrock(x*) = 318463.4738773398 , Gradient Rosenbrock(x*) = [-199077.77552647 -11284.80476644]
Gradient Descent Method by Analytical Differentiation: Global minimum is (x,y)=(a,a^2) for f(x,y)=0
a = 1 , b = 100 , x0 = [-0.5, 4.0] -> x* = [0.99900158 0.99800016] @itr = 4505
@Rosenbrock(x*) = 9.98444170387427e-07 , Gradient Rosenbrock(x*) = [-0.00039937 -0.00079954]
Newton Method by Automatic Differentiation
a = 1 , b = 100 , x0 = [-0.5, 4.0] -> x* = [1. 1.] @itr = 6
@Rosenbrock Gradient (x*) = [ 4.35207426e-14 -2.22044605e-14]
@Rosenbrock AD Hessian(x*) = [[ 802. -400.] [-400. 200.]]
Gradient Descent Method by Automatic Differentiation
a = 1 , b = 100 , x0 = [-0.5, 4.0] -> x* = [0.99900238 0.99800175] @itr = 4506
@Rosenbrock Function (x*) = 9.98444170387427e-07
@Rosenbrock AD Gradient(x*) = [-0.00039937 -0.00079954]参考までに、ローゼンブロック関数の最小化に至る過程(図中”+”)の可視化グラフを添付する。ニュートン法はたった5回で最適解に至るため面白みに欠ける故、最急降下法によるグラフも併せて引用する。


Closing-toward Julia Programming Language
Python言語による実装ADは、Pythonがインタープリター形式であることから演算に時間が掛かることを再認識した。又、コードはシンプルに記述できるものの、之まで用いてきたFortran、C++の静的型付けに慣れている俺にとてはPythonの動的型付けにもAssertに不安を覚える。将来的にはiSMARTをPythonで書換え、自動微分を組込むことを目論んでいたが一気にやる気を喪失する。
C++での実装も考えたがEasy-Readableな言語でないことからこれも乗り気にならない。代替言語を探した挙句、比較的新しい言語のJuliaを使って見ようという気になる。
JuliaはC、Fortran、MATLABの良いとこ取りした言語で技術計算、機械学習、データサイエンスに長ける。コンパイル方式でPython、C、Fortranのライブラリも直接Callすることができる。又、Juliaはコード実行前に型推論/最適化を行う動的な型システムであるが別途変数に対して型指定できる利点もある。
一層のこと、気持ちも新たにFortan仕様のiSMARTをJuliaに書き換えよう。Julia仕様jSMARTとでも名付けて書換え作業を通じて残る人生の楽しみの糧にしようか?その前にJulia版ADIをご紹介しよう。
「冬籠りヘタルなと鼓舞する椿 自動微分の日々花開く」

References
- コラム:自動微分 — DeZero Book
- Neidinger, R. 2010. Introduction to automatic differentiation and MATLAB object-oriented programming. SIAM Review, 52(3), 545–563. doi:10.1137/080743627
- An Introduction to Reservoir Simulation Using MATLAB/GNU Octave: User Guide for the MATLAB Reservoir Simulation Toolbox (MRST), Cambridge University Press, c2019
- Bezanson, J., Karpinski, S., Shah, V., Edelman, A., 2012. Why we created julia. Accessed 21.11.2018. URL https://julialang.org/blog/2012/02/why-we-created-julia
- JuliaDiff: Differentiation tools in Julia. JuliaDiff on GitHub
- Julia 1.8 Documentation
- Sindre Grøstad, June 2019. Automatic Differentiation in Julia with Applications to Numerical Solution of PDEs. Master’s thesis in Applied Physics and Mathematics, NTNU
〆