寄り道第二回目のテーマは行列式。ドイツの哲学者ライプニッツが行列の祖として知られていますが、愕くことなかれ、それに先立つこと十年前、我が国算聖関孝和が著書「解伏題之法」で自ら発見した行列式の理論を紹介しています。

行列式の導入

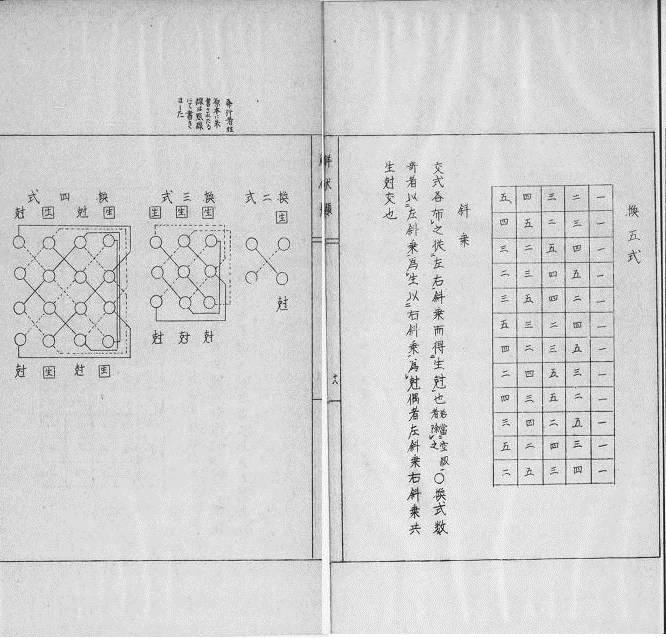
行列式の算法は「解伏題之法」の第五生尅斜乗に記載されています。

国立国会図書館近代デジタルライブラリー

漢文縦書きで記載されていますので、 読みやすく横書きにすると、

交式、 各之を布きて、 左右の斜乗により 生剋（正負）を得る也。 換式数奇なるものは、 左斜乗を以って生となし、 右斜乗を以って剋となす。 偶なるものは、 左斜乗、 右斜乗共に生剋相交わる也。

国立国会図書館近代デジタルライブラリー

関孝和が考案した算法のうち三次式は、世界的に著名なフランスの数学者サラスの方法と全く同等です。サラスの発見は孝和に遅れる事163年後の1846年になります。

具体的には、三次元行列\(A\)、$$ \begin{equation} A= \begin{pmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{pmatrix} \end{equation} $$の行列式\(detA\)は次式で与えられる。

$$ \begin{align}
detA  &= \begin{vmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{vmatrix} 
\\ &= a_{11}  \begin{vmatrix} a_{22}&a_{23}\\ a_{32}&a_{33} \end{vmatrix} – a_{12} \begin{vmatrix} a_{21}&a_{23}\\ a_{31}&a_{33} \end{vmatrix} + a_{13} \begin{vmatrix} a_{21}&a_{22}\\ a_{31}&a_{32} \end{vmatrix} 
\\ &= a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32}
\\ &- ( a_{13}a_{22}a_{31} + a_{12}a_{21}a_{33} + a_{11}a_{23}a_{32} )
\end{align} $$

関孝和の図同様、非常に美しい公式であることが分かります。

詰り、左上から右下に向かう方向に「+」、右上から左下に向かう方向に「－」の符号を付けて積を取りそれらの和を取ることで、行列式の値を求めることができます。因みに、「解伏題之法」では右から始まるので正負（生尅）は逆となっている。

連立方程式の解法

次に連立方程式の解法を考えてみましょう。

古典的な解法の一つであるクラメルの公式を用いると、連立方程式 \({Ax=b}\)の解は、\( x_i= \displaystyle \frac{detA_i}{detA} \)で与えられる。

ここで、\(xi\)は数列\(x\)の第\(i\)成分であり、行列\(Ai\)は行列\(A\)の第\(i\)列の部分を数列\(b\)にしたものである。

例えば、三次式の場合、以下と同義である。

$$ \begin{align}　x_1 = \frac { \begin{vmatrix} b_{1}&a_{12}&a_{13}\\ b_{2}&a_{22}&a_{23}\\ b_{3}&a_{32}&a_{33} \end{vmatrix}} {detA}
,\ \  x_2 = \frac { \begin{vmatrix} a_{11}&b_{1}&a_{13}\\ a_{21}&b_{2}&a_{23}\\ a_{31}&b_{3}&a_{33} \end{vmatrix}} {detA}
, \ \  x_3 = \frac { \begin{vmatrix} a_{11}&a_{12}&b_{1}\\ a_{21}&a_{22}&b_{2}\\ a_{31}&a_{32}&b_{3} \end{vmatrix}} {detA} \end{align} $$

サラスの公式同様、非常に美しい。

プログラミングの実際

クラメルの公式は三次迄を適用しているが、四次以上になると計算量が多くなって実用的でないので、ガウスの消去法による解法が一般的である。

subroutine MINVRT(Org, Inv, Noe, EPSMAC)
!********************************************************************************
!*	Square Matrix Inversion Routine                                         *
!********************************************************************************
    implicit none
    integer::	Noe
    real*8::	det,    div
    real*8::	b1,     b2,     b3,     b4,     b5,     b6,     b7,     b8,     b9
    real*8::	Org(Noe,Noe),	Inv(Noe,Noe)
!================================================================================
!   Inversion by the cramel method
!================================================================================
	if  (Noe == 1) then

		det = Org(1,1)
		if (abs(det) <= EPSMAC) then
			write(*,'("@Warning: Inverse of the diagonal matrix is zero!")')
			det = EPSMAC
		endif
		Inv(1,1) = 1.0 / det

	else if (Noe == 2) then

		det = Org(1,1) * Org(2,2) - Org(2,1) * Org(1,2)
		if (abs(det) <= EPSMAC) then
			write(*,'("@Warning: Inverse of the diagonal matrix is zero!")')
			det = EPSMAC
		endif
		div = 1.0 / det
		Inv(1,1) =   div * Org(2,2)
		Inv(1,2) = - div * Org(1,2)
		Inv(2,1) = - div * Org(2,1)
		Inv(2,2) =   div * Org(1,1)

	else if (Noe == 3) then

		b1 = Org(2,2) * Org(3,3) - Org(2,3) * Org(3,2)
		b2 = Org(1,3) * Org(3,2) - Org(1,2) * Org(3,3)
		b3 = Org(1,2) * Org(2,3) - Org(1,3) * Org(2,2)
		b4 = Org(2,3) * Org(3,1) - Org(2,1) * Org(3,3)
		b5 = Org(1,1) * Org(3,3) - Org(1,3) * Org(3,1)
		b6 = Org(1,3) * Org(2,1) - Org(1,1) * Org(2,3)
		b7 = Org(2,1) * Org(3,2) - Org(2,2) * Org(3,1)
		b8 = Org(1,2) * Org(3,1) - Org(1,1) * Org(3,2)
		b9 = Org(1,1) * Org(2,2) - Org(1,2) * Org(2,1)

		det = Org(1,1) * b1 + Org(2,1) * b2 + Org(3,1) * b3
		if (abs(det) <= EPSMAC) then
			write(*,'("@Warning: Inverse of the diagonal matrix is zero!")')
			det = EPSMAC
		endif
		div = 1.0 / det

		Inv(1,1) =   div * b1
		Inv(1,2) =   div * b2
		Inv(1,3) =   div * b3
		Inv(2,1) =   div * b4
		Inv(2,2) =   div * b5
		Inv(2,3) =   div * b6
		Inv(3,1) =   div * b7
		Inv(3,2) =   div * b8
		Inv(3,3) =   div * b9
!================================================================================
!   Inversion by the gaussian elimination
!================================================================================
	else
		.....
	endif
!================================================================================
end subroutine

このガウスの消去法は疎行列解法の根幹をなす解法で、本Scientific Programmingの究極のテーマでもある。

次回はまた寄り道するか、本題に戻るか、分かりませんが、よろしく。

つづく