温暖な北陸の冬籠りを経て春を過ぎ初夏目前の梅雨入りのこの頃、半年以上に亘って追求してきたが、iSMARTに自動微分を組込むことが上手く行かず頓挫状態にある。只、その試行錯誤する合間、単変数坑井モデルのiSMARTに対して解析微分に基づくヤコビ行列を実装することになってしまったことは愛嬌か。本末転倒の取組みになってしまい本来の目的を達成することができなかったことで気分的にはスッキリしないが、結果オーライで良しとしよう。さて、残る”SMARTSOL”の重要論点である強結合坑井モデルの行列解法につき説明する。After a mild winter in Hokuriku, spring has passed quickly and the rainy season has just begun before summer, I am struggling to implement automatic differentiation in iSMART, although I have been working on it for more than half a year. I have not been able to figure out the fatal reason for the failure. During the trial and error period, however, I ended up incorporating the analytical Jacobian into the one-solution-variable well model in iSMART. It’s a charm, isn’t it? It is not pleasant for me to fail to achieve the initial goal, but I am happy with the result. Now it would be a time to address the strongly coupled well model for the remaining important issue of the matrix solution method.

貯留層ヤコビ行列と坑井ヤコビ行列を強結合して得られる強結合係数行列を解く事によって坑井の解の安定性を確保する事は以前延べたが､本章では強結合係数行列の処理方法を取り扱う。

今､強結合係数行列を

$$ \begin{equation}
\begin{pmatrix}
J_{RR} & J_{RW} \\
J_{WR} & J_{WW}
\end{pmatrix}
\begin{pmatrix}
X_{R} \\ X_{W}
\end{pmatrix}
=
\begin{pmatrix}
R_{R} \\ R_{W}
\end{pmatrix}
\end{equation} \tag{8.1}$$

とする。ここで、
\(X_{R}\)：貯留層解
\(X_{W}\)：坑井解
\(R_{R}\)： 貯留層残差
\(R_{W}\)：坑井残差

上式において\(J_{RW}\)を消去すると次式に整理される。

$$ \begin{equation}
\begin{pmatrix}
J^{’}_{RR} & 0 \\
J_{WR} & J_{WW}
\end{pmatrix}
\begin{pmatrix}
X_{R} \\ X_{W}
\end{pmatrix}
=
\begin{pmatrix}
R^{‘}_{R} \\ R_{W}
\end{pmatrix}
\end{equation} \tag{8.2}$$

ここで、
$$\begin{align}J_{RR}^{’} &= J_{RR} – J_{RW} J_{WW}^{-1} J_{WR} \\ \tag{8.3} \\
R_{R}^{’} &= R_{R} – J_{RW} J_{WW}^{-1} R_{W} \end{align}$$

故に､坑井解\(X_{W}\)は次式から決定される。

$$X_{W} = J^{-1}_{WW}(R_{W} – J_{WR}R_{W}) \tag{8.4}$$

念の為、図8.5に例題のグリッドシステムを再掲する。

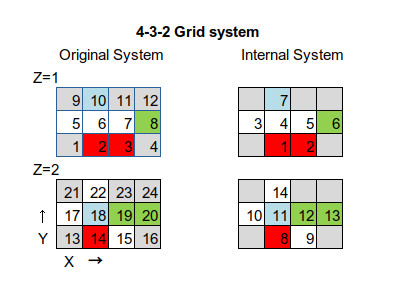
図8.6に強結合係数行列の非零成分の配置を示す｡

解くべき変数の数の違いによる非零成分の配置構成を理解する為､坑井１は変数３個､坑井２については変数１個に設定している｡条件として、坑井がある格子は全てFIM近似する必要がある。

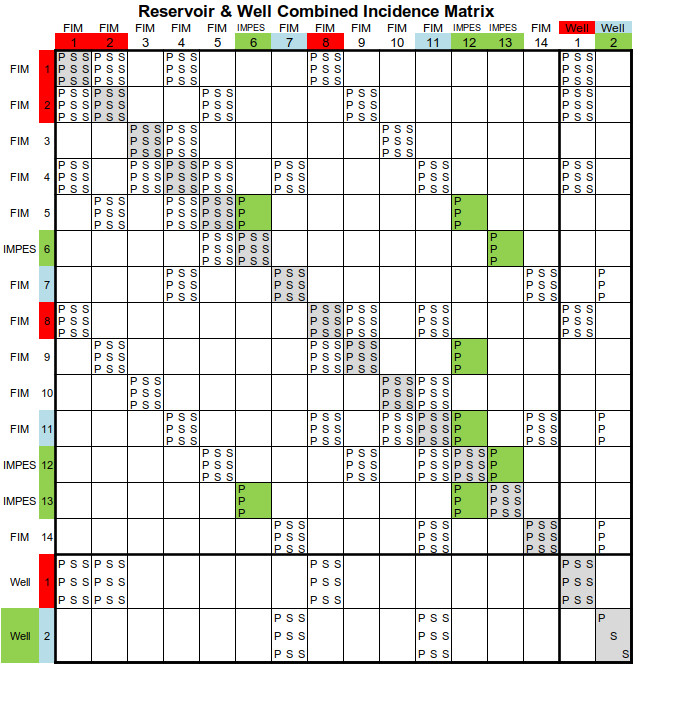
坑井１は解くべき変数は３個なので､行列\(J_{WR}\)、\(J_{RW}\)、\(J_{WW}\)共、３ｘ３のフル小行列となる｡一方、坑井２に於いては、\(J_{WR}\)、\(J_{RW}\)、\(J_{WW}\)は\(P_{w}^{n+1}\)による偏微分しか存在しない為、３x１の小行列となる。
行列\(J_{WR}\)は、\(J_{WR}=\sum_{j∈i}∂q_{\ell,j}/∂X_{R,m,k}\)から、３ｘ１の小行列となる。

尚、ガウス消去法のようなILU前処理では､強結合係数行列の数値解を求めようとする場合、

$$J{’}_{RR} =J_{RR}-J_{RW} – J^{-1}_{WW}J_{WR} \tag{8.7}$$

の操作によって坑井ヤコビ行列を分離することにより､元の非零成分の位置と異なった位置に非零成分が形成される｡この為、どの位置に新しく非零成分がフィルイン(掃き出されるか)、前もって把握しておく必要がある。このためILU前処理方法はNF前処理方法に比べて手数が掛かることになる。

これにて、Matrix Solver構築に当たって必要とされる前処理並びに重要事項の説明は全て終了となる。次回からは反復解法をテーマにする予定。

その前にBlack Oil Simulator最大のテーマである坑井モデルの実装につき詳説する所存。乞うご期待！

以上
つづく