“SMARTSOL”の重要論点の一つである順応陰解法(AIM)に関してシリーズでご紹介します。第一回目は行列解法に於けるAIM法の取り扱い方法について説明します。I would like to address about the Adaptive Implicit Method (AIM) in series, which is one of the main functions incorporated in SMARTSOL. In this first thread, we will discuss how to implement the AIM method in the matrix solver.

貯留層(Reservoir)に於けるヤコビ行列\(J_{RR}\)は次のように表されることはご既承の通り。

$$J_{RR}=\frac{\partial \Delta M_{R,\ell,i}}{\partial X_{R,m,i}} – \sum_{j∈i}\frac{\partial F_{\ell,j}}{\partial X_{R,m,i}} + \frac{\partial q_{\ell,i}}{\partial X_{R,m,i}} \tag{7.0}$$

依って、ヤコビ行列においては、蓄積項(Accumulation Term)\(\partial \Delta M_{R,\ell,i}/\partial X_{R,m,i}\)とソース項(Source Term)\(\partial q_{\ell,i}/\partial X_{R,m,i}\)は対象格子の変数のみから成り立っており、流れ項(Flow Term)\(\sum_{j∈i}\partial F_{\ell,j}/\partial X_{R,m,i}\)に関しては対象格子\(i\)と隣接格子\(j\)の双方の変数から成立している事が確認できる。

列(Column)毎にAIM係数行列を実際に構築してみよう。
蓄積項は対象格子の変数が全て時刻\(n+1\)にて評価される為、格子がFIM(Fully Implcit)格子であろうとIMPES(Implicit Pressure Explicit Saturation)格子であろうと\((P_{o},S_{w},S_{g})^{n+1}\)による偏微分が存在するので、AIM係数行列の対角成分は零を含まないフル行列となる。

次に、AIM係数行列の非対角成分の小行列について検討してみよう。
先ず、IMPES格子\(i\)とFIM格子\(j\)間の流れ項を考える｡格子\(j\)がFIM格子である為､格子\(i\)には\((P_{o,j},S_{w,j},S_{g,j})^{n+1}\)による非対角流れの偏微分が生じる｡しかし､FIM格子\(j\)を対象に考えた場合､格子\(i\)はIMPES格子であるから\(S_{w,j},S_{g,i}\)が関与する流れ項は全て時刻\(n\)で評価される事になる。故に、\((P_{o,i},S_{w,i},S_{g,i})^{n+1}\)による非対角流れの偏微分は表われず､\((P_{o,i})^{n+1}\)による非対角流れの偏微分のみ対応Columnに形成される事になる。

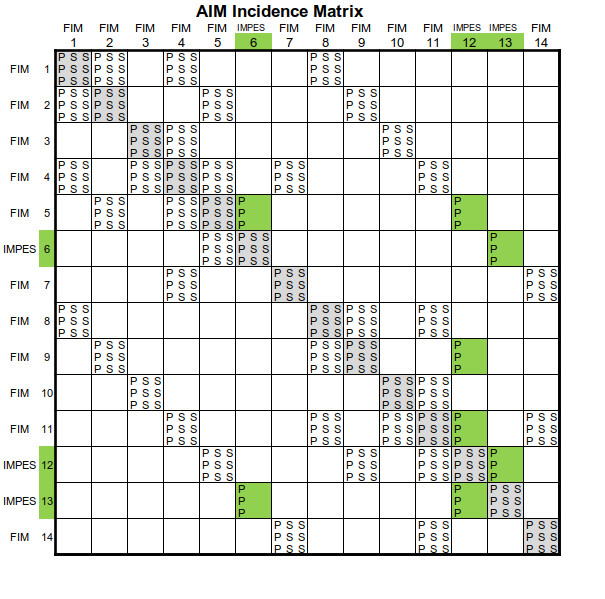
例題に於けるAIM係数行列を図7.1に示す。

同図において\(P\)は貯留層圧力、\(S\)は飽和によるヤコビの小行列を示している。このようにFIM格子については３X３=９の小行列が､IMPES格子については３X１=３の小行列が非対角成分のColumnに各々形成される。

解法に当たっては、置換行列(Permutation Matrix)を導入し、AIM係数行列\(J\)を次のように変形させ、陽変数と陰変数とに分割する。

$$ \begin{equation} PJP^{T} =
\begin{pmatrix}
J_{EE} & J_{EI} \\
0 & J_{II}
\end{pmatrix}
\end{equation} \tag{7.2}$$

ここで、
\(J_{EE}~\)対角小行列で陽変数の小行列より構成
\(J_{EI}~~\)行に陰変数､列に陽変数から構成される非対角小行列
\(J_{II}~~~\)陰変数の小行列から構成。\(J_{II}\)の非零成分は元のAIM係数行列と同位置

更に､解を\(X\)、残差を\(R\)とすると次式が成り立つ。

$$ \begin{equation}
\begin{pmatrix}
J_{EE} & J_{EI} \\
0 & J_{II}
\end{pmatrix}
\begin{pmatrix}
X_{E} \\ X_{I}
\end{pmatrix}
=
\begin{pmatrix}
R_{E} \\ R_{I}
\end{pmatrix}
\end{equation} \tag{7.3}$$

詰まり､AIM係数行列の数値解法は、先ず\(J_{II}X_{I}=R_{I}\)から陰変数\(X_{I}\)を求め、次に\(X_{E}=J_{EE}^{-1}(R_{E}-J_{EE}X_{I})\)から後退代入法にて陽変数\(X_{E}\)を解く事になる。

ここで、計算を簡便化すると共に丸め誤差を低減する為に、行各々の対角行列の逆行列をAIM係数行列に前もって掛け、陰係数行列をスケーリングしておく｡これにより\(J_{EE}\)は単位行列となる。

以上、AIM係数行列に行各々の対角行列の逆行列を掛けた後､行と列を適宜変換する事で、最終的に図7.4のような縮小行列を得る。

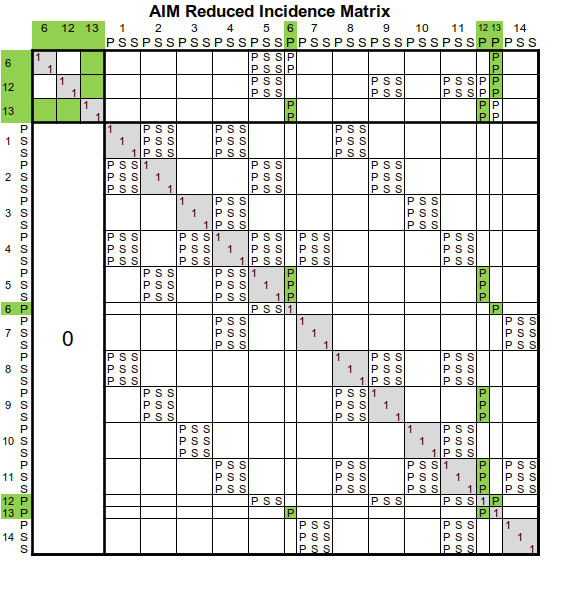
Matrix Solver構築に於いてAIM法の処理方法の説明はこれで終了。次回は、自家製シミュレータiSMART･SMARTにおけるAIM法の実装方法並びに挙動結果につきご紹介する。

以上
つづく