
SMART〜The Well Model
上流石油産業に於いて複雑で精微な坑井オペレーションが追求されたことを受けて、実態を正確に反映する坑井モデリングがリザーバーシミュレーションに不可欠な要素となった。しかしながら、従前の一般的な坑井モデルでは坑井内の多相流動モデルの再現性が限定的であった。これを受けて提唱された”Multi Segment Well Model (MSWell)”は現実的な坑井挙動に近づける坑井内に於ける物性の再現性の向上を図る技法であるものの、貯留層と強結合されるMSWell坑井モデルは多相流動方程式の同時解法の困難さを伴い実用的な技法であるとは言い難い。依って、Inhouse SMARTシミュレータにはMSWellモデルを導入していないものの、将来拡張を視野に多変数(3変数)を扱える坑井モデルを組み込んでいる。 Accurate well modeling becomes essential in the reservoir simulation because more complex well operations are employed in the petroleum industry. The prevailed standard well model is proved to be computationally efficient, while it lacks the ability to capture the multiphase flow details within the wellbore. MultiSegment well (MSWell) model is then proposed to approximate the actual physical shape of the well and perform accurate simulation within the wellbore. However, the increasing complexity of the MSWell model introduces additional difficulties in solving the strongly coupled MSWell and reservoir flow problem. Therefore, the inhouse SMART simulator in which the MSWell model is not incorporated adopts the three-solution-variable well model in light of the future expansion.
Preface
陰解法リザーバーシミュレータ(Implicit Reservoir Simulator)に於ける強結合坑井モデルは確立された技術である。強結合坑井モデルとは貯留層独立変数に加えて坑井独立変数を解変数として追加し、貯留層と坑井の多相流体方程式を強結合の上、貯留層独立変数(圧力と飽和率)と同時に坑底圧力を求める技法である。長期のTime Stepに於ける数値安定性を維持しつつ坑井の生産・圧入ターゲットを同時に正しく満足することを可能とする。
一般的に強結合坑井モデルでは坑底圧力のみを解くべき坑井独立変数としているが、業界標準シミュレータ”ECLIPSE”では更に2変数を解くべき独立変数として追加して貯留層と同様に3変数とし坑井挙動の再現性の向上を図っている。これによって一義的に坑井の仕上げ層を介して貯留層内で発生する逆流(Cross flow)現象を正確に再現できるとしている。
一方、Coatsらの論考では従来の坑底圧力のみを解くべき独立変数とした1変数坑井モデルでも”ECLIPSE”の算定ロジックを導けることを証明している。確かに、黎明期に開発された坑底圧力のみを独立変数とする坑井モデルの場合でも実用的な精度で逆流現象を再現できる事から今でも幅広く用いられている技法である。
独立変数が少ないほど演算処理時間が迅速となり且つ収束性は損なわれない優位性がある。只、小規模な対象に於いては俺のしょぼいパソコンやタブレットでも1変数でも3変数でも演算速度はそれほど変わらない。
先ず本章でCoatsらが提唱する”Fully Mixed Wellbore Saturation Model”を説明する。便宜上表記を適宜変更の上引用する。
坑井の仕上げ層\(k\)に於ける相\(m\)の流量\(q\)は次式で与えられる。
$$q_{m,k} = J_{k} λ_{m,k} (P_{K} − P_{wb} )\tag{1.0}$$
坑井の坑底圧力\(Pwb\)は式(1.0)より式(1.1)が求まる。
$$p_{wb} =\frac{\displaystyle \sum_{k=1}^{n}J_{k}λ_{k}P_{K} − \sum_{k=1}^{n} \sum_{m} q_{m,k}}{\displaystyle \sum_{k=1}^{n} J_{k} λ_{k}}\tag{1.1}$$
坑底圧力\(P_{wb}\)が貯留層圧力\(P_{k}\)より高い場合、逆流現象が発生するので、InflowとOutflow状態で上流の易動度が異なる。依って、式(1.0)に”Upstream Mobility” \(λ_{m,k}^{ups}\)を導入して易動度を次式のように表す。
$$q_{m,k} = J_{k} λ_{m,k}^{ups}(P_{K} − P_{wb} )\tag{1.2}$$
尚、下表1.3にてInflowとOutflowの各々の易動度につき整理する。地上状態ではなく、地下の坑井状態に於ける易動動を求めることに留意すること。
| Upstream Mobility | Outflow | Inflow |
| \(λ_{m,k}^{ups}\) | \(f_{m} λ_{t,k}\) | \(λ_{m,k}\) |
ここで、 \(f_{m}\)は仕上げ層各々に関与しない坑内平均飽和率”Fully Mixed Wellbore Saturation”を示す。\(f_{m}\)は次式から容易く求まる。\(+(sum)\)とはInflowが発生する仕上げ層に於ける流量の総和を示す。
$$f_{m} =\frac{q_{m}^{+}}{\displaystyle \sum_{m}q_{m}^{+}}\tag{1.4}$$
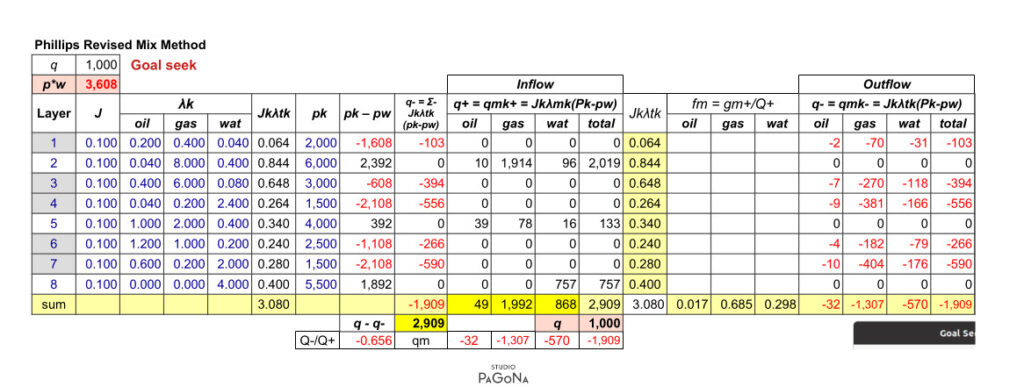
Coatsらの論考をSimulateするSpread Sheetを下表1.5に添付する。坑井内の平均飽和率は坑井容積を考慮せずとも求まることが理解できよう。
Three-Solution-Variable Well Model
本稿の本題である多変数(3)坑井モデルについて説明しよう。
基本的な考え方についてはECLIPSEの論文をReferしているが、本章で改めて整理しておく。
Strongly Coupled Implicit Well Model
強結合坑井陰解法とは貯留層物質保存式と坑井物質保存式を合体した非線形連立方程式\(R(X)\)に対して、貯留層独立変数と坑井独立変数の解\(X\)をニュートン反復法にて同時に求めることである。
先ず、非線形方程式\(R(X)\)に対してニュートン法にて第\(k\)近似解を中心にテイラー展開にて線形化する。テイラー展開において第3項以降を無視すると次式が得られる。
$$R(X_{ k+1}) = R(X_{k}+ΔX) = R(X_{k}) + R'(X_{k})ΔX\tag{2.0}$$
上式が零になるようにするには、修正量\(ΔX = −R(X_{k})/R'(X_{k})\)とすればいい。即ち、求めるべき解\(X_{k+1}\)は残差ベクトルに対するニュートン法によって次式から求められる。
$$X_{k+1} = X_{k} + ΔX_{k}\tag{2.1}$$
$$ΔX = −\frac{R(X_{k})}{R'(X_{k})}\tag{2.2}$$
ここで、微分値の集合、ヤコビ行列\(J_{k} = R'(X_{k})\)を導入すると次式に帰着する。
$$J_{k}ΔX_{k} = R(X_{k})\tag{2.3}$$
貯留層と坑井との合成ヤコビ行列、及び非線形連立方程式\(R(X)\)は次式で構成される。
$$\left|\begin{array}{c|c} J_{RR}&J_{RW} \\ \hline J_{WR}&J_{WW}\end{array}\right|
\left |\begin{array} {c} X_{R,l} \\\hline X_{W,l} \end{array} \right| =
\left |\begin{array} {c} R_{R,m} \\\hline R_{W,m} \end{array} \right| \tag{2.4}$$
貯留層及び坑井共々3相・3独立変数を扱うヤコビ行列の具体的な構成偏微分は以下で示される。
$$\begin{align} J_{RR}=\frac{δR_{R,m}}{δX_{R,l}}=\begin{vmatrix}
\frac{δR_{R,o}}{δX_{R,1}} & \frac{δR_{R,o}}{δX_{R,2}} & \frac{δR_{R,o}}{δX_{R,3}} \\
\frac{δR_{R,w}}{δX_{R,1}} & \frac{δR_{R,w}}{δX_{R,2}} & \frac{δR_{R,w}}{δX_{R,3}} \tag{2.5a}\\
\frac{δR_{R,g}}{δX_{R,1}} & \frac{δR_{R,g}}{δX_{R,2}} & \frac{δR_{R,g}}{δX_{R,3}}
\end{vmatrix} \end{align}$$
$$\begin{align} J_{RW}=\frac{δR_{R,m}}{δX_{W,l}}=\begin{vmatrix}
\frac{δR_{R,o}}{δX_{W,1}} & \frac{δR_{R,o}}{δX_{W,2}} & \frac{δR_{R,o}}{δX_{W,3}} \\
\frac{δR_{R,w}}{δX_{W,1}} & \frac{δR_{R,w}}{δX_{W,2}} & \frac{δR_{R,w}}{δX_{W,3}} \tag{2.5b}\\
\frac{δR_{R,g}}{δX_{W,1}} & \frac{δR_{R,g}}{δX_{W,2}} & \frac{δR_{R,g}}{δX_{W,3}}
\end{vmatrix} \end{align}$$
$$\begin{align} J_{WR}=\frac{δR_{W,m}}{δX_{R,l}}=\begin{vmatrix}
\frac{δR_{W,o}}{δX_{R,1}} & \frac{δR_{W,o}}{δX_{R,2}} & \frac{δR_{W,o}}{δX_{R,3}} \\
\frac{δR_{W,w}}{δX_{R,1}} & \frac{δR_{W,w}}{δX_{R,2}} & \frac{δR_{W,w}}{δX_{R,3}} \tag{2.5c}\\
\frac{δR_{W,g}}{δX_{R,1}} & \frac{δR_{W,g}}{δX_{R,2}} & \frac{δR_{W,g}}{δX_{R,3}}
\end{vmatrix} \end{align}$$
$$\begin{align} J_{WW}=\frac{δR_{W,m}}{δX_{W,l}}=\begin{vmatrix}
\frac{δR_{W,o}}{δX_{W,1}} & \frac{δR_{W,o}}{δX_{W,2}} & \frac{δR_{W,o}}{δX_{W,3}} \\
\frac{δR_{W,w}}{δX_{W,1}} & \frac{δR_{W,w}}{δX_{W,2}} & \frac{δR_{W,w}}{δX_{W,3}} \tag{2.5d}\\
\frac{δR_{W,g}}{δX_{W,1}} & \frac{δR_{W,g}}{δX_{W,2}} & \frac{δR_{W,g}}{δX_{W,3}}
\end{vmatrix} \end{align}$$
Three Phase Mass Conservation Equation
先に述べた貯留層に於ける多相物質保存方程式は次式(3.0)で与えられる。
$$\displaystyle R_{R,m,i} = ΔM_{R,m,i} – \sum_{j∈i}F_{m,j} + q_{m,i}\tag{3.0}$$
ここで、\(ΔM_{R,m,i}\)はTime Step\(Δt\)当たりの貯留層格子グリッド\(i\)に於ける貯留層蓄積項の変化量、\(\displaystyle \sum_{j∈i}F_{m,j}\)は隣接格子グリッド\(j\)からの格子グリッド\(i\)へのネット流量を表す流れ項、\(q_{m,i}\) は貯留層格子グリッド\(i\)に仕上げ層を有する坑井の総生産量を示すソース項である。
一方、坑井に於ける多相物質保存方程式は次式(3.1)で示さる。各坑井\(i\)、各相\(m\)毎に設定する。$$\displaystyle R_{W ,m,i} = ΔM_{W,m,i} – \sum_{j∈i} q_{m,j} + Q_{m,i}\tag{3.1}$$
同じく、\(ΔM_{W ,m,i}\)はTime Step\(Δt\)当たりの坑井\(i\)に於ける坑井蓄積項の変化量である。\( \displaystyle \sum_{j∈i} q_{m,j}\)は仕上げ層格子グリッド\(j\)から坑井\(i\)への流れ項の流量を表す。\(Q_{m,i}\)は坑井\(i\)に於ける各相\(m\)の総生産・圧入量を示すソース項である。流量\(q\)及び\(Q\)は生産では正、圧入では負とする。詰まり、坑井の物質保存方程式は貯留層と同等となる。
坑井のヤコビ行列を下表3.2に示す。詳細な偏微分値の展開は略す。
| Jacobian | Formula |
| \(J_{WW}\) | \( \displaystyle \frac{ δR_{W,m,i}}{δX_{W,l,k}} = \frac{δΔM_{W,m,i}}{ X_{W,l,i}} − \sum_{j∈i}\frac{δq_{m,j}}{δX_{W,l,j}} + \frac{δQ_{m,i}}{δX_{W,l,i}}\) |
| \(J_{WR}\) | \( \displaystyle \frac{ δR_{W,m,i}}{δX_{R,l,k}} = − \sum_{j∈i}\frac{δq_{m,j}}{δX_{R,l,j}}\) |
| \(J_{RW}\) | \(\displaystyle \frac{ δR_{R,m,i}}{δX_{W,l,k}} = \frac{δq_{m,i}}{X_{W,l,i}} = \frac{δq_{m,i}}{δP_{wb,etc}}\frac{δP_{wb,etc}}{X_{W,l,i}}\) |
Well Primary Variables
坑井の独立変数を下表4.0に設定する。
\(P_{wb}\)は坑底圧、\(F_{w}\)と\(F_{g}\)は坑井内に於ける其々水とガスの流動比率、\(Q_{T}\)は坑井の生産・圧入量を示す。
| Solution Variable | Rate Control | THP・BHP Control |
| \(X_{W,1}\) | \(P_{wb}\) | \(Q_{T} = λ_{o} Q_{o} + λ_{w} Q_{w} + λ_{g} Q_{g}\) |
| \(X_{W,2}\) | \(F_{w}\) | \(F_{w}\) |
| \(X_{W,3}\) | \(F_{g}\) | \(F_{g}\) |
THP・BHP制御坑井に於いては、流量を坑井独立変数として適用した方が便利なので、坑底圧力\(P_{wb}\)の代わりに流量\(Q_{T}\)を導入する。その際のヤコビ行列の変更は下記演算ロジックで編成して対応する。
$$\frac{δR}{δX_{W,1}} ≒ \frac{δR}{δX_{W,1}} + \frac{δP_{wb}}{δX_{W,1}} \frac{δR}{P_{wb}}\tag{4.1}$$
上式に於いて、 BHP制御坑井では偏微分\(δP_{wb}/δX_{W,1}\)は零となる。 THP制御坑井に於いては、偏微分\(δP_{wb}/δX_{W,1}\)は”Tubing Inflow Performance”の勾配と\(δ(WFR)/δF_{w}\)等から求まる。
各坑井の生産挙動を次式で表す。係数\(F_{w}\) と\(F_{g}\) を使うことで坑井挙動を忠実に再現できる。$$\begin{align}
F_{o} &= 1 − F_{w} − F_{g} \\
F_{w}&= \frac{λ_{w} Q_{w}}{λ_{o} Q_{o}+λ_{w} Q_{w}+λ_{g} Q_{g}}\tag{4.2} \\
F_{g} &= \frac{λ_{g} Q_{g}}{λ_{o} Q_{o}+λ_{w} Q_{w}+λ_{g} Q_{g}}
\end{align}$$
更に、生産井の各相の生産量が等価になるように重み付けを行う。SMARTの各相の単位を油\(rb\),水\(rb\),ガス\(Mcf\)と設定していることを踏まえて各相の重み係数を次式のように設定している。
$$\begin{align}
λ_{o} &= 1.0 \\
λ_{w} &= 1.0 \tag{4.3} \\
λ_{g} &= 0.001・ガス係数=0.1781076
\end{align}$$
因みに、貯留層の独立変数は下表4.4の通り。
| Solution Variable | Saturated Oil & Gas | Undersaturated Oil | Undersaturated Gas |
| \(X_{R,1}\) | \(P_{X}\) | \(P_{X}\) | \(P_{X}\) |
| \(X_{R,2}\) | \(S_{w}\) | \(S_{w}\) | \(S_{w}\) |
| \(X_{R,3}\) | \(S_{g}\) | \(R_{s}\) | \(R_{v}\) |
\(P_{X}\)は貯留層圧力である。
Well Mass Accumulation Term
坑井の容積(坑井蓄積量)は微少であるものの完全に無視すると、坑井独立変数の行列式が特異解の状態に陥る恐れが生じるらしい。依って、相\(m\)毎に”Well Volume Factor”\(ν\)なる概念を導入する。本導入によっても収束性を損なう恐れは限定的。坑底状態に於ける単位体積当たりの各相のStock Tank容積として表す。
Well Volume Factorは坑井に於ける\(P_{wb}\),\(F_{w}\), \(F_{g}\)から容易く算定される。
Well Flow Term
坑井と坑井仕上げ層格子グリッド間の流路を”Well Connection”と呼び、式(3.1)で与えた仕上げ層\(j\)に於ける相\(m\)の流量は次式で与えられる。
$$q_{m,j} = J_{w,j} λ_{m,j} (P_{X,j} – P_{wb} – H_{w,j} )\tag{5.0}$$
ここで、\(J_{w,j}\)は仕上げ層格子グリッド\(j\)と坑井間の伝達率(Transmissibility)による”Productivity Index”を示し、\(λ_{m,j}\)は仕上げ層格子グリッド\(j\)に於ける相\(m\)の易動度(Mobility)を示す。括弧内の圧力差は仕上げ層格子グリッドで生ずる圧力のDrawdownを示す。\(H\)は”Hydrostatic Head”である。
仕上げ層格子グリッドに於ける(地層から坑壁へ流入する)易動度\(\)は次式で与えられる。
$$λ_{m} = \frac{K_{rm}}{B_{m}μ_{m}}\tag{5.1}$$
ここで、仕上げ層格子グリッドに於ける相対浸透率\(K_{r}\) 、容積係数\(B\)、及び粘度\(μ\)である。
圧入に対しては上流方向に於ける飽和率を反映するように易動度\(λ\)を修正する必要がある。逆流がない場合、圧入層は単相状態となるので、掛かる状況下では式(5.1)の\(K_{rm}/μ_{m}\)は相の総和で置き換えられる。
$$λ_{m} =\frac{1}{B_{m}}\bigg \lbrack \frac{K_{ro}}{μ_{o}} + \frac{K_{rw}}{μ_{w}} + \frac{K_{rg}}{μ_{g}} \bigg \rbrack \tag{5.2}$$
ここで、添字\(m\)は圧入対象相を示す。上式のように所謂”Injectivity”は仕上げ層格子グリッドに於ける”Total Fluid Mobility”として取り扱う。
多層仕上げ坑井に於いては、ある仕上げ層に於けるDrawdownが他の仕上げ層に対して流入方向が逆転する場合に逆流現象が発生することは良く知られている。逆流現象が発生すると、仕上げ層を通して混合流体が流入する。例えば、水圧入井では地層から油が坑井内に流れ込み水と混合することも起こりうる。或いは、逆流現象が発生している生産井では或る地層から油ガス混合物が他の層に圧入されうる。これらの状況に対応する為、坑井内に於ける混合流体を適切に再現できるように”Injection Mobility”を修正する必要がある。
ここで、坑井内に亘って流体の状態は均一と仮定する。即ち、各相のWell Volume Factorに応じて圧入される。圧入混合流体の性状は同一、且つ混合流体の”Total Injectivity”は仕上げ層格子グリッドに於けるTotal Fluid Mobilityに依存すると見做すと、Injection Mobilityは次式で与えられる。
$$λ_{m} =\frac{(K_{ro}/μ_{o}+K_{rw}/μ_{w}+K_{rg}/μ_{g})}{ν_{fo}B_{o}+ν_{w} B_{w}+ν_{fg}B_{g}}ν_{m}\tag{5.3}$$
ここで、 \(ν_{fo}\)と\(ν_{fg}\) は各々、坑井内の”Free Oil”乃至は”Free Gas”のWell Volume Factor, を示す。単相の場合、式(5.3)は式(5.2)に簡略する。
Well Source Term
坑井ターゲット設定値\(Q_{T}\)を用いて坑井のソース項を定める。
生産若しくは圧入流量は坑井の制御モードによって異なる。
一例として油生産流量制御の生産井に於ける各相の生産流量を下表6.0で示す。
\(Q_{T}\)はターゲットの油生産流量設定値である。水生産流量制御、ガス生産流量制御、及び液体(油+水)生産流量制御生産井に於ける関係式も容易く導き出される。油層状態での流量制御坑井に対しては平均油層状態に換算した上で流量を算定する。圧入井では対象とする相の圧入流量である。
更に、油生産流量制御坑井に於いて坑底圧力が低下し油生産量が維持できなくなって坑底乃至坑口圧力(BHP・THP)制御に移行する場合に於ける生産・圧入量は下表で示す。
| Phase Rate | Oil Rate Control Producer | Oil Rate Control Injector |
| Oil | \(Q_{T}\) | \(-Q_{T}\) |
| Wat | \((F_{w}/λ_{w})(λ_{o}/F_{o})*Q_{T}\) | \(-R_{s}Q_{T}\) |
| Gas | \((F_{g}/λ_{g})(λ_{o}/F_{o})*Q_{T}\) | 0 |
THP制御坑井に於ける生産・圧入量は流動状態を規定する坑口圧力\(P_{wt}\)並びに関連パラメータから構成する坑底圧力算定式(Lookup_Table)から”Tubing Inflow Performance Curve”の内挿補間法により求める。
$$P_{wb} = LookupTable(P_{wt} , Q_{T} , WFR, GFR)\tag{6.2}$$
ここで、 \(Q_{T}\)は所与の相(液体,ガス等)の流量を指す。\(WFR\) は水の比率を規定する変数(含水率等)を表す。同様に、\(GFR\) はガス比率を規定する変数(ガス液比等)を表す。
| Phase Rate | BHP Control Producer | THP Control Producer | BHP・THP Control Injector |
| Oil | \(F_{o}/λ_{o}*Q_{T} \) | \(Q_{T} \) | \(-Q_{T}\) |
| Wat | \(F_{w}/λ_{w}*Q_{T} \) | \((F_{w}/λ_{w})(λ_{o}/F_{o})*Q_{T} \) | \(-R_{s}Q_{T}\) |
| Gas | \(F_{g}/λ_{g}*Q_{T} \) | \((F_{g}/λ_{g})(λ_{o}/F_{o})*Q_{T} \) | 0 |
その他の関係式についてはHolmesのPaperを参照されたし。
One-Solution-Variable Well Model
最後に、iSMARTの坑井モデルである単変数坑井モデルに触れておく。
坑井の独立変数を坑底圧力\(P_{wb}\)と仮定することは最初に述べたように、同坑底圧力から各相の流量制御、THP制御、BHP制御等のあらゆる坑井制御に対応できる。
多変数坑井モデルと単変数坑井モデルの関連算定式の差異は規定するResidual Equation に起因する。
| Well Variable | Control Mode | Residual Equation |
| One | Rate BHP | \(R_{W} = Q_{W} ^{Update}−Q_{W}^{Target}\) \(R_{W} = P_{W,wb} ^{Update}−P_{W,wb}^{Target}\) |
| Three | – | \(\displaystyle R_{W,t,i} =\sum_{m=o,w,g}(ΔM_{W,m,i} – \sum_{j∈i} q_{m,j} + Q_{m,i})= 0\) |
単変数坑井モデルの関連式を下表に示す。
| Item | Rate or BHP Control |
| \(X_{W,l}\) | \(P_{wb}\) |
| \(J_{WW}\) | \(ΔQP/ΔX_{W,l}\) |
| \(J_{WR}\) | \(ΔQ/ΔR_{x,l}\) |
| \(J_{RW}\) | \(ΔQ_{i}/ΔX_{W,l}\) |
因みに、坑井の容積は不要であるが、重み付けは多変数坑井モデル同様に設定している。
参考までに、多変数坑井モデルに置ける関連式を下表に整理しておく。
| Item | |
| \(R\) | \(\displaystyle R_{W,t,i} =\sum_{m=o,w,g}(ΔM_{W,m,i} – \sum_{j∈i} q_{m,j} + Q_{m,i})\) |
| \(X_{W,1}\) | Rate Control: \(P_{wb}\) BHP・THP Control: \(Q_{t}=λ_{o}Q_{o}+λ_{w}Q_{w}+λ_{g}Q_{g}\) |
| \(X_{W,2}\) | \(F_{w}\) |
| \(X_{W,3}\) | \(F_{g}\) |
| \(J_{WW}\) | \(\displaystyle δR_{W,t,i}/δX_{W,1} = \sum_{m=o,w,g}δ(ΔM_{W,m,i} – \sum_{j∈i} q_{m,j} + Q_{m,i})/δX_{W,1}\) |
| \(J_{WR}\) | \(\displaystyle δR_{W,t,i}/δX_{R,m,k} = δ(ΔM_{W,m,i} – \sum_{ j∈i} q_{m,j} + Q_{m,i} )/δX_{R,m,i} =–\sum_{m=o,w,g} \sum_{j∈i} δq_{m,j}/δX_{R,m,i}\) |
| \(J_{RW}\) | \(\displaystyle δR_{R,m,i}/δX_{W,1} = δ(ΔM_{R,m,i} – \sum_{j∈i} F_{m,j} + q_{m,i} )/δX_{W,1}\) |
強結合坑井モデルに於いても多変数の場合、先ず坑井戸の解をInner Iterationによって求めておく方が結果的に収束性が良くなることが知られている。実装の手法として、坑井解の反復法Iteration(Inner)を経てから、貯留層を含めた全体解を反復解(Outer Iteration)によって求めることになる。一方、単変数坑井モデルでは坑井のInner Iterationは不要で一気に全体(貯留層+坑井)の解を反復法にて求める。
Closing
SMART Simulatorには解析微分によるヤコビ行列を組込んでいる。貯留層に対するヤコビ行列の算定は然程困難ではないが、坑井モデルの諸制御下に置ける偏微分の算定には非常に苦慮し多大な時間を費やした。若気の至りのチャレンジであったが、懐かしい思い出で今でも鮮明に覚えている。
さて、半年以上に亘って自動微分に基づくiSMARTの開発を追求してきたが、上手く行かずデッドロック状態にある。梅雨明け10日の山行で気分を一新して再度取り掛かろうと思っている。

以上
Seize the day!
Appendix
Reference
- Holmes,J.A.:“Enhancement to the Strongly Coupled, Fully Implicit Well Model: Wellbore Crossflow Modeling and Collective Well Control,” SPE12259, 1983.
- Modline,A.D., Coats,K.H., and Wells,M.W.:”A Super Position Method for Representing Wellbore Crossflow in Reservoir Simulation” SPERE, August 1992.
- Coats,K.H., Thomas,L.K., and Pierson,R.G.:“Compositional and Black Oil Reservoir Simulation,” SPE29111, 1995.
- Holmes,J.A., Barkve,T., and Lund,O.:”Application of a multisegment well model to simulate flow in advanced well,” SPE50646, 1998.
Nomenclature
\(B\): Formation Volume Factor, stb/rb
\(f\),\(F\): Phase Flow Ratio, fraction
\(H\): Hydrostatic Head, psia
\(J_{λ}\): Well Connection Mobility, RB/D-psi
\(J_{k}\): Well Production Index (Transmissibility) at Layer\(k\) , RB-cp/D-psi
\(k\): Well layer \(k = 1, … , n\)
\(K_{r}\): Relative Permeability, fraction
\(P\),\(P_{X}\): Reservoir Pressure, psia
\(P_{wh}\): Well Head Flowing Pressure, psia
\(P_{wb}\): Well Bottomhole Flowing Pressure, psia
\(q\): Flow Rate, RB/D
\(q_{t}\): Total Flow Rate, RB/D, \(q_{t}=q_{o}+q_{w}+q_{g}\)
\(S\): Saturation, fraction
\(T_{k,j}\): Transmissibility between layer\(k\)and\(j\), RB-cp/D-psi
\(Δt\): Time Step
\(X\): Solution Variables
\(μ\): Viscosity, cp
\(λ\): Mobility, cp-1, \(λ = K_{r}/(μB)\)
\(λ_{t}\): Total Mobility, cp-1 , \(λ_{t} = λ _{o}+ λ_{w}+ λ_{g}\)
\(\sum^{+}\): For all inflow layer
\(sum^{-}\): For all outflow layer
\(J\): Jacobian Matrix
\(M\): Mass Accumulation Term
\(Q\): Well Source Term, Flow Rate, RB/D
\(F\): Flow Term
\(R\): Reservoir
\(W\): Well
\(m\): Oil, Water, or Gas phase Identifier
\(l\): Well Variable Identifier
\(t\): Total
\(T\): Target
〆